Matrix< T > Class Template Reference

#include <Matrix++.h>

Collaboration diagram for Matrix< T >:
Collaboration graph
[legend]

List of all members.

Public Member Functions

 Matrix ()
 Matrix (int nn,...)
virtual ~Matrix ()
 関数にコピー渡しした場合に，関数内でディストラクトされても良い様に free() は使用しない．
void init ()
void init (int nn,...)
void getm (int nn, int *size)
T & element (int i,...)
void clear (T v=T(0))
void dup (Matrix< T > a)
void free ()
 free() は手動で呼び出す．

Public Attributes

int n
 次元数
int r
 全要素数 sz[0]*sz[1]*...*sz[n-1]
int d
 汎用
int * sz
 各次元の要素数 sz[0] 〜 sz[n-1]
T * mx
 要素 mx[0] 〜 mx[r-1]
T err
 エラー時にこれを参照用として返す．

Detailed Description

template<typename T = double>
class jbxl::Matrix< T >

template <typename t="double"> class Matrix

多次元マトリックス型 Matrix
  • 注: Matrix型の引数は (行, 列, ....)となるので，直接メモリにアクセスする場合は注意が必要である．
  • 2次元(3x3)の場合...., (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), ....
  • 3次元(2x2x2)の場合... (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), ....

Definition at line 34 of file Matrix++.h.

Constructor & Destructor Documentation

Matrix (  )  [inline]

Definition at line 45 of file Matrix++.h.

00045 { init();}

Matrix ( int  nn,
  ... 
) [inline]

template <typename t>=""> Matrix<T>::Matrix(int nn, ...)

コンストラクタ

Parameters:
nn マトリックスの次元数．
... 各次元の要素数．
例
    Matrix(1, 4)      --- 4元ベクトル
    Matrix(2, 3, 4)   --- 3x4 の2次元マトリックス
    Matrix(3, 2, 4, 3) -- 2x4x3 の3次元マトリックス

Definition at line 78 of file Matrix++.h.

References Matrix< T >::d, Matrix< T >::err, Matrix< T >::free(), Matrix< T >::mx, Matrix< T >::n, Matrix< T >::r, and Matrix< T >::sz.

00079 {
00080     r   = 0;
00081     n   = nn;
00082     d   = 0;
00083     err = (T)0;
00084     mx  = NULL;
00085     sz  = (int*)malloc(n*sizeof(int));
00086     if (sz==NULL) return;
00087 
00088     va_list argsptr;
00089 
00090     va_start(argsptr, nn);
00091     r = 1;
00092     for (int i=0; i<n; i++) {
00093         sz[i] = (int)va_arg(argsptr, int);
00094         r = r*sz[i];
00095     }
00096     va_end(argsptr);
00097 
00098     mx = (T*)malloc(r*sizeof(T));
00099     if (mx==NULL) {
00100         ::free(sz);
00101         sz = NULL;
00102         return;
00103     }
00104     for (int i=0; i<r; i++) mx[i] = (T)0;
00105     
00106     return;
00107 }

Here is the call graph for this function:

virtual ~Matrix (  )  [inline, virtual]

Definition at line 47 of file Matrix++.h.

Member Function Documentation

void clear ( T  v = T(0)  )  [inline]

Definition at line 54 of file Matrix++.h.

00054 { for(int i=0;i<r;i++) mx[i]=v;}

void dup ( Matrix< T >  a  )  [inline]

Definition at line 55 of file Matrix++.h.

00055 { *this = dup_Matrix(a);}

T & element ( int  i,
  ... 
) [inline]

template <typename t>=""> T& Matrix<T>::element(int i, ...)

Matrix の要素を返す．次元数に制限はない．インデックスは1から数える（0からではない）．

参考
1次元配列へのアクセスインデックス 
    1次元: element(i)                                                                    (i-1)
    2次元: element(i,j)                                        (j-1) +             sz[1]*(i-1)
    3次元: element(i,j,k)                  (k-1) +       sz[2]*(j-1) +       sz[1]*sz[2]*(i-1)
    4次元: element(i,j,k,l)  (l-1) + sz[3]*(k-1) + sz[2]*sz[3]*(j-1) + sz[1]*sz[2]*sz[3]*(i-1)
    ...................

Definition at line 213 of file Matrix++.h.

References Matrix< T >::d, Matrix< T >::err, Matrix< T >::free(), Matrix< T >::mx, Matrix< T >::n, Matrix< T >::r, and Matrix< T >::sz.

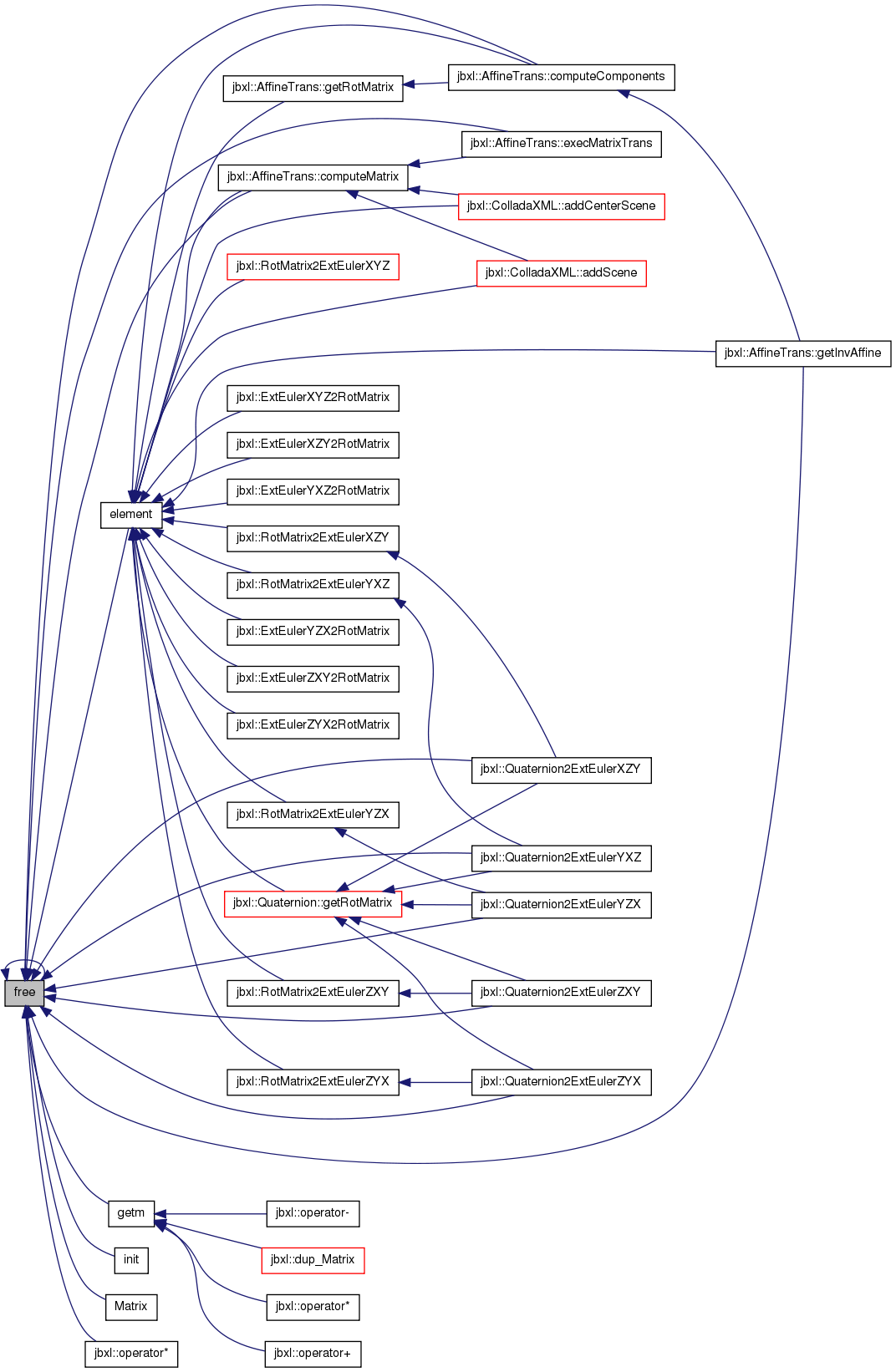
Referenced by ColladaXML::addCenterScene(), ColladaXML::addScene(), AffineTrans< T >::computeComponents(), AffineTrans< T >::computeMatrix(), jbxl::ExtEulerXYZ2RotMatrix(), jbxl::ExtEulerXZY2RotMatrix(), jbxl::ExtEulerYXZ2RotMatrix(), jbxl::ExtEulerYZX2RotMatrix(), jbxl::ExtEulerZXY2RotMatrix(), jbxl::ExtEulerZYX2RotMatrix(), AffineTrans< T >::getInvAffine(), AffineTrans< T >::getRotMatrix(), Quaternion< T >::getRotMatrix(), jbxl::RotMatrix2ExtEulerXYZ(), jbxl::RotMatrix2ExtEulerXZY(), jbxl::RotMatrix2ExtEulerYXZ(), jbxl::RotMatrix2ExtEulerYZX(), jbxl::RotMatrix2ExtEulerZXY(), and jbxl::RotMatrix2ExtEulerZYX().

00214 {
00215     int*  args;
00216     va_list argsptr;
00217         
00218     args = (int*)malloc(n*sizeof(int));
00219     if (args==NULL) return err;
00220 
00221     va_start(argsptr, i);
00222     args[0] = i;
00223     for (int m=1; m<n; m++) {
00224         args[m] = (int)va_arg(argsptr, int);
00225     }
00226     va_end(argsptr);
00227 
00228     int dx = args[0] - 1;
00229     for (int d=1; d<n; d++) dx = dx*sz[d] + args[d] - 1;
00230     ::free(args);
00231 
00232     if (dx>=r || dx<0) return err;
00233     return mx[dx];
00234 }

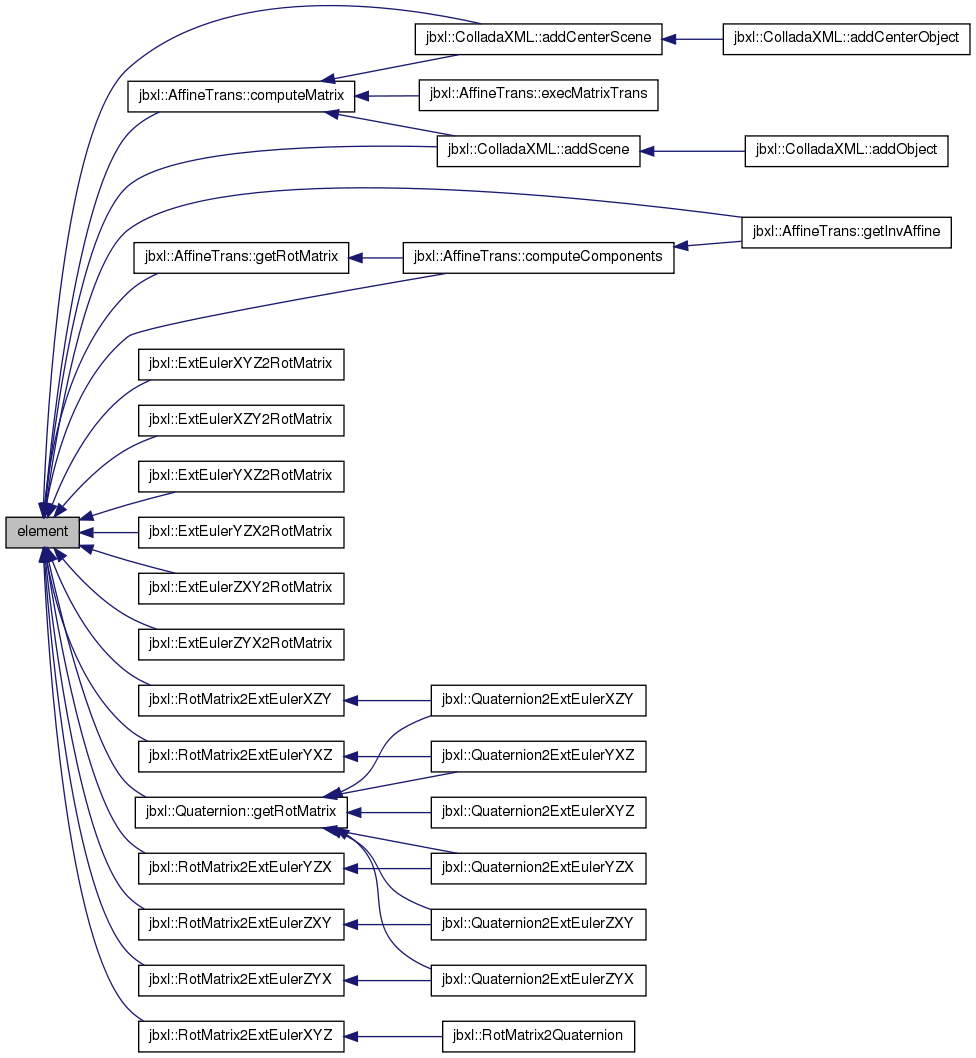
Here is the call graph for this function:

Here is the caller graph for this function:

void free ( void   )  [inline]

Definition at line 58 of file Matrix++.h.

Referenced by AffineTrans< T >::computeComponents(), AffineTrans< T >::computeMatrix(), Matrix< T >::element(), AffineTrans< T >::execMatrixTrans(), Matrix< double >::free(), AffineTrans< T >::getInvAffine(), Matrix< T >::getm(), Matrix< T >::init(), Matrix< T >::Matrix(), jbxl::operator*(), jbxl::Quaternion2ExtEulerXZY(), jbxl::Quaternion2ExtEulerYXZ(), jbxl::Quaternion2ExtEulerYZX(), jbxl::Quaternion2ExtEulerZXY(), and jbxl::Quaternion2ExtEulerZYX().

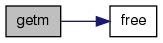
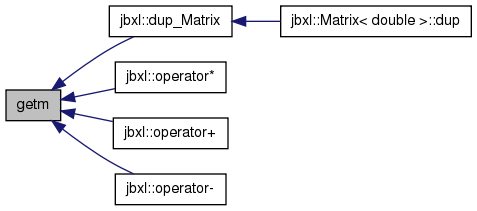
00058 { if(sz!=NULL) ::free(sz); if(mx!=NULL) ::free(mx); init();}

Here is the caller graph for this function:

void getm ( int  nn,
int *  size 
) [inline]

template <typename t>=""> void Matrix<T>::getm(int nn, int* size)

現在のバッファ部をクリアして，任意(n)次元の実数マトリックスのバッファ部をつくり出す．
要素自体は (T)0に初期化される．init() とは引数の形が違うだけ

Parameters:
nn マトリックスの次元数．
size size[0]〜size[nn-1]: 各次元の要素数．

Definition at line 165 of file Matrix++.h.

References Matrix< T >::d, Matrix< T >::err, Matrix< T >::free(), Matrix< T >::mx, Matrix< T >::n, Matrix< T >::r, and Matrix< T >::sz.

Referenced by jbxl::dup_Matrix(), jbxl::operator*(), jbxl::operator+(), and jbxl::operator-().

00166 {
00167     if (size==NULL) return;
00168     if (sz!=NULL) ::free(sz);
00169     if (mx!=NULL) ::free(mx);
00170 
00171     r   = 0;
00172     n   = nn;
00173     d   = 0;
00174     err = (T)0;
00175     mx  = NULL;
00176     sz  = (int*)malloc(n*sizeof(int));
00177     if (sz==NULL) return;
00178 
00179     r = 1;
00180     for (int i=0; i<n; i++) {
00181         sz[i] = size[i];
00182         r = r*sz[i];
00183     }
00184 
00185     mx = (T*)malloc(r*sizeof(T));
00186     if (mx==NULL) {
00187         ::free(sz);
00188         sz = NULL;
00189         return;
00190     }
00191     for (int i=0; i<r; i++) mx[i] = (T)0;
00192 
00193     return;
00194 }

Here is the call graph for this function:

Here is the caller graph for this function:

void init ( int  nn,
  ... 
) [inline]

template <typename t>=""> void Matrix<T>::init(int nn, ...)

現在のバッファ部をクリアして，任意(n)次元の実数マトリックスのバッファ部をつくり出す．
要素自体は (T)0に初期化される．現在のバッファ部をクリアする以外は，コンストラクタと同じ．

Parameters:
nn マトリックスの次元数．
... 各次元の要素数．

Definition at line 120 of file Matrix++.h.

References Matrix< T >::d, Matrix< T >::err, Matrix< T >::free(), Matrix< T >::mx, Matrix< T >::n, Matrix< T >::r, and Matrix< T >::sz.

00121 {
00122     if (sz!=NULL) ::free(sz);
00123     if (mx!=NULL) ::free(mx);
00124 
00125     r   = 0;
00126     n   = nn;
00127     d   = 0;
00128     err = (T)0;
00129     mx  = NULL;
00130     sz  = (int*)malloc(n*sizeof(int));
00131     if (sz==NULL) return;
00132 
00133     va_list argsptr;
00134 
00135     va_start(argsptr, nn);
00136     r = 1;
00137     for (int i=0; i<n; i++) {
00138         sz[i] = (int)va_arg(argsptr, int);
00139         r = r*sz[i];
00140     }
00141     va_end(argsptr);
00142 
00143     mx = (T*)malloc(r*sizeof(T));
00144     if (mx==NULL) {
00145         ::free(sz);
00146         sz = NULL;
00147         return;
00148     }
00149     for (int i=0; i<r; i++) mx[i] = (T)0;
00150     
00151     return;
00152 }

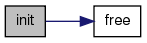
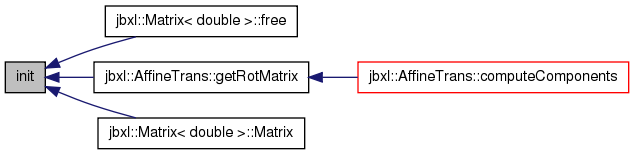
Here is the call graph for this function:

void init ( void   )  [inline]

Definition at line 49 of file Matrix++.h.

Referenced by Matrix< double >::free(), AffineTrans< T >::getRotMatrix(), and Matrix< double >::Matrix().

00049 { n = r = d = 0; err = (T)0; sz = NULL; mx = NULL;}

Here is the caller graph for this function:

Member Data Documentation

int d

Definition at line 39 of file Matrix++.h.

Referenced by jbxl::dup_Matrix(), Matrix< T >::element(), Matrix< T >::getm(), Matrix< T >::init(), Matrix< double >::init(), and Matrix< T >::Matrix().

T err

Definition at line 42 of file Matrix++.h.

Referenced by jbxl::dup_Matrix(), Matrix< T >::element(), Matrix< T >::getm(), Matrix< T >::init(), Matrix< double >::init(), and Matrix< T >::Matrix().

T* mx

Definition at line 41 of file Matrix++.h.

Referenced by Matrix< double >::clear(), jbxl::dup_Matrix(), Matrix< T >::element(), AffineTrans< T >::execMatrixTrans(), Matrix< double >::free(), Matrix< T >::getm(), Matrix< T >::init(), Matrix< double >::init(), Matrix< T >::Matrix(), jbxl::operator*(), jbxl::operator+(), jbxl::operator-(), jbxl::operator/(), jbxl::operator==(), and jbxl::print_Matrix().

int n

Definition at line 37 of file Matrix++.h.

Referenced by jbxl::dup_Matrix(), Matrix< T >::element(), Matrix< T >::getm(), Matrix< T >::init(), Matrix< double >::init(), jbxl::isSameDimension(), Matrix< T >::Matrix(), jbxl::operator*(), jbxl::operator+(), jbxl::operator-(), jbxl::operator/(), and jbxl::print_Matrix().

int r

Definition at line 38 of file Matrix++.h.

Referenced by Matrix< double >::clear(), jbxl::dup_Matrix(), Matrix< T >::element(), Matrix< T >::getm(), Matrix< T >::init(), Matrix< double >::init(), jbxl::isSameDimension(), Matrix< T >::Matrix(), jbxl::operator*(), jbxl::operator+(), jbxl::operator-(), jbxl::operator/(), jbxl::operator==(), and jbxl::print_Matrix().

int* sz

Definition at line 40 of file Matrix++.h.

Referenced by jbxl::dup_Matrix(), Matrix< T >::element(), Matrix< double >::free(), Matrix< T >::getm(), Matrix< T >::init(), Matrix< double >::init(), jbxl::isSameDimension(), Matrix< T >::Matrix(), jbxl::operator*(), jbxl::operator+(), jbxl::operator-(), jbxl::operator/(), and jbxl::print_Matrix().

The documentation for this class was generated from the following file:
Generated on 15 Nov 2023 for JunkBox_Lib++ (for Windows) by  doxygen 1.6.1