Lib/matrix.c File Reference

マトリックス＆ベクトルライブラリ More...

#include "matrix.h"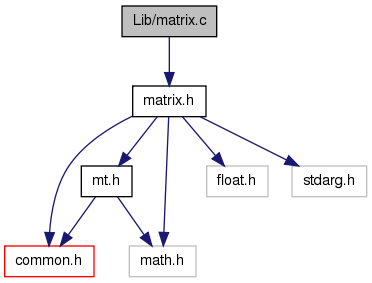

Include dependency graph for matrix.c:

Go to the source code of this file.

Functions
vector	unit_vector (vector a)
vector	unit_ivector (ivector a)
vector	set_vector (double x, double y, double z)
ivector	set_ivector (int x, int y, int z)
ivector	f2ivector (vector a)
vector	i2vector (ivector a)
vector	ex_vector (vector a, vector b)
matrix	make_matrix1 (int n)
imatrix	make_imatrix1 (int n)
matrix	make_matrix2 (int n, int m)
imatrix	make_imatrix2 (int n, int m)
matrix	make_matrix (int n, int *sz)
imatrix	make_imatrix (int n, int *sz)
void	free_matrix (matrix *a)
void	free_imatrix (imatrix *a)
double *	get_matrix (matrix mtx,...)
int *	get_imatrix (imatrix mtx,...)
void	copy_matrix (matrix src, matrix dst)
void	copy_imatrix (imatrix src, imatrix dst)
matrix	add_matrix (matrix a, matrix b)
imatrix	add_imatrix (imatrix a, imatrix b)
matrix	sub_matrix (matrix a, matrix b)
imatrix	sub_imatrix (imatrix a, imatrix b)
matrix	mlt_matrix (matrix a, matrix b)
imatrix	mlt_imatrix (imatrix a, imatrix b)
void	print_matrix (FILE *fp, matrix a)
void	print_imatrix (FILE *fp, imatrix a)
matrix	decompQR (matrix xx, imatrix col)
matrix	minimum2 (matrix y, matrix x)
matrix	trans_matrix (matrix a)
matrix	invrU_matrix (matrix x)

---

Detailed Description

Author:

Fumi.Iseki (C)

Definition in file matrix.c.

---

Function Documentation

imatrix add_imatrix	(	imatrix	a,
		imatrix	b
	)

imatrix add_imatrix(imatrix a, imatrix b)

マトリックスの足し算． 整数マトリックス a, bを足し算して,結果の整数マトリックスを返す．

Parameters:

	a	足されるマトリックス．
	b	足すマトリックス．

Returns:

足し算結果の整数マトリックス．

Definition at line 610 of file matrix.c.

References make_imatrix(), imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

{
    int  i;
    imatrix c;

    c.n = c.r = 0;
    c.sz = NULL;
    c.mx = NULL;
    if (a.mx==NULL || b.mx==NULL) return c;
    if (a.r != b.r)               return c;

    c = make_imatrix(a.n, a.sz);
    for (i=0; i<c.r; i++) c.mx[i] = a.mx[i] + b.mx[i];
    return c;
}

Here is the call graph for this function:

matrix add_matrix	(	matrix	a,
		matrix	b
	)

matrix add_matrix(matrix a, matrix b)

マトリックスの足し算． 実数マトリックス a, bを足し算して,結果の実数マトリックスを返す．

Parameters:

	a	足されるマトリックス．
	b	足すマトリックス．

Returns:

足し算結果のマトリックス．

Definition at line 582 of file matrix.c.

References make_matrix(), matrix::mx, matrix::n, matrix::r, and matrix::sz.

{
    int  i;
    matrix c;

    c.n = c.r = 0;
    c.sz = NULL;
    c.mx = NULL;
    if (a.mx==NULL || b.mx==NULL) return c;
    if (a.r != b.r)               return c;

    c = make_matrix(a.n, a.sz);
    for (i=0; i<c.r; i++) c.mx[i] = a.mx[i] + b.mx[i];
    return c;
}

Here is the call graph for this function:

void copy_imatrix	(	imatrix	src,
		imatrix	dst
	)

void copy_imatrix(imatrix src, imatrix dst)

整数マトリックスのコピー．srcの内容を dstへコピーする．
マトリックス全体のサイズが合わない場合は何もしない．
全体のサイズが合っていればコピーする．

Parameters:

	src	コピー元マトリックス．
	dst	コピー先マトリックス．

Definition at line 559 of file matrix.c.

References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

{
    int  i;

    if (src.mx==NULL  || dst.mx==NULL)  return;
    if ((src.r!=dst.r)||(dst.n!=dst.n)) return;

    for (i=0; i<src.n; i++) dst.sz[i] = src.sz[i];
    for (i=0; i<src.r; i++) dst.mx[i] = src.mx[i];
}

void copy_matrix	(	matrix	src,
		matrix	dst
	)

void copy_matrix(matrix src, matrix dst)

マトリックスのコピー．srcの内容を dstへコピーする．
マトリックス全体のサイズが合わない場合は何もしない．
全体のサイズが合っていればコピーする．

Parameters:

	src	コピー元マトリックス．
	dst	コピー先マトリックス．

Definition at line 536 of file matrix.c.

References matrix::mx, matrix::n, matrix::r, and matrix::sz.

{
    int  i;

    if (src.mx==NULL  || dst.mx==NULL)  return;
    if ((src.r!=dst.r)||(dst.n!=dst.n)) return;

    for (i=0; i<src.n; i++) dst.sz[i] = src.sz[i];
    for (i=0; i<src.r; i++) dst.mx[i] = src.mx[i];
}

matrix decompQR	(	matrix	xx,
		imatrix	col
	)

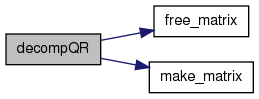
matrix decompQR(matrix xx, imatrix col)

2次元行列 xxのQR分解を行い,R行列を返す．

xx = Q・R

• xxのQR分解を行った後,係数のマトリックス(上三角行列 R)を返す．
• ピボット操作（列の入れ換え）をした場合は整数ベクトル colに Qの 基底ベクトルが入る．
• colは予め make_imatrix()等によって確保されていなければならない．

Parameters:

	xx	QR分解を行う2次元行列．
	col	メモリを確保し,初期化しておく．Qの基底ベクトルが入る．

Returns:

上三角行列 R

Definition at line 881 of file matrix.c.

References free_matrix(), make_matrix(), Mx, imatrix::mx, matrix::mx, matrix::n, matrix::r, imatrix::sz, matrix::sz, and Vt.

Referenced by minimum2().

{
    int    i, j, r, n, m, sz[2];
    double s, t, u;
    matrix  nsq, isq, x, a;

    a.n = a.r = 0;
    a.sz = NULL;
    a.mx = NULL;
    if (xx.mx==NULL || col.mx==NULL)      return a;
    if (xx.n!=2 || (xx.sz[1]!=col.sz[0])) return a;
    
    nsq.mx = isq.mx = x.mx = NULL;
    n = xx.sz[0];
    m = xx.sz[1];
    sz[0] = sz[1] = m;
    nsq = make_matrix(1, &m);
    isq = make_matrix(1, &m);
    x   = make_matrix(xx.n, xx.sz);
    a   = make_matrix(xx.n, sz);
    if (nsq.mx==NULL || isq.mx==NULL || x.mx==NULL || a.mx==NULL) {
        free_matrix(&nsq); 
        free_matrix(&isq); 
        free_matrix(&x); 
        return a;
    }

    for (i=0; i<xx.r; i++) x.mx[i] = xx.mx[i];

    for (i=1; i<=m; i++) {
        for (s=0.0,j=1; j<=n; j++) s = s + Mx(x, j, i)*Mx(x, j, i);
        Vt(nsq, i) = s;
        Vt(isq, i) = ((Vt(nsq, i)!=0) ? Vt(nsq,i) : -1.0);
        Vt(col, i) = i;
    }

    for (r=1; r<=m; r++) {
        if (r!=1) {
            j = r; u = 0.0;
            for (i=r; i<=m; i++) {
                t = Vt(nsq,i)/Vt(isq,i);
                if (t>u) { u = t; j = i; }
            }
            i = Vt(col,j); Vt(col,j) = Vt(col,r); Vt(col,r) = i;
            t = Vt(nsq,j); Vt(nsq,j) = Vt(nsq,r); Vt(nsq,r) = t;
            t = Vt(isq,j); Vt(isq,j) = Vt(isq,r); Vt(isq,r) = t;
            for (i=1; i<=n; i++) {
                t = Mx(x,i,j);
                Mx(x,i,j) = Mx(x,i,r);
                Mx(x,i,r) = t;
            }
        }

        for (u=0.0,i=r; i<=n; i++) u = u + Mx(x,i,r)*Mx(x,i,r);
        u = sqrt(u); 
        if (Mx(x,r,r)<0.0) u = -u;
        Mx(x, r, r) = Mx(x,r,r) + u; 
        t = 1.0/(Mx(x,r,r)*u);

        for (j=1; j<=r-1; j++) Mx(x,r,j)=0.0;
        for (j=r+1; j<=m; j++) {
            for (s=0.0,i=r; i<=n; i++) s = s + Mx(x,i,r)*Mx(x,i,j);
            for (i=r; i<=n; i++) Mx(x,i,j) = Mx(x,i,j) - s*t*Mx(x,i,r);
        }
        Mx(x,r,r) = -u;
    }

    for (i=1; i<=m; i++) {
        for (j=1; j<=m; j++) Mx(a,i,j) = Mx(x,i,j);
    }

    free_matrix(&nsq);
    free_matrix(&isq);
    free_matrix(&x);

    return a;
}

Here is the call graph for this function:

Here is the caller graph for this function:

vector ex_vector	(	vector	a,
		vector	b
	)

vector ex_vector(vector a, vector b)

ベクトルの外積． 実数ベクトル a,b の外積ベクトルを計算し,それを返す．

Parameters:

	a	外積を計算するベクトル．
	b	外積を計算するベクトル．

Returns:

外積ベクトル．

Definition at line 175 of file matrix.c.

References vector::n, vector::x, vector::y, and vector::z.

{
    vector c;

    c.x = a.y*b.z - a.z*b.y;
    c.y = a.z*b.x - a.x*b.z;
    c.z = a.x*b.y - a.y*b.x;
    c.n = sqrt(c.x*c.x+c.y*c.y+c.z*c.z);
    return c;
}

ivector f2ivector

(

vector

a

)

ivector f2ivector(vector a)

実数ベクトル a から整数ベクトルをつくり出し,それを返す． 各要素は四捨五入される．

Parameters:

a

変換する実数ベクトル．

Returns:

変換された整数ベクトル．

Definition at line 131 of file matrix.c.

References ivector::n, vector::x, ivector::x, vector::y, ivector::y, vector::z, and ivector::z.

{
    ivector c;

    c.x = (int)(a.x + 0.5);
    c.y = (int)(a.y + 0.5);
    c.z = (int)(a.z + 0.5);
    c.n = sqrt((double)c.x*c.x + c.y*c.y + c.z*c.z);
    return c;
}

void free_imatrix

(

imatrix *

a

)

void free_imatrix(imatrix* a)

整数マトリックスのバッファ部を開放する．

Parameters:

a

開放するバッファ部を持った整数マトリックスへのポインタ．

Definition at line 435 of file matrix.c.

References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

Referenced by minimum2().

{
    if(a->sz!=NULL) free(a->sz);
    if(a->mx!=NULL) free(a->mx);
    a->sz = NULL;
    a->mx = NULL;
    a->n  = a->r  = 0;
}

Here is the caller graph for this function:

void free_matrix

(

matrix *

a

)

void free_matrix(matrix* a)

マトリックスのバッファ部を開放をする．

Parameters:

a

開放するバッファ部を持ったマトリックスへのポインタ．

Definition at line 417 of file matrix.c.

References matrix::mx, matrix::n, matrix::r, and matrix::sz.

Referenced by decompQR(), and minimum2().

{
    if(a->sz!=NULL) free(a->sz);
    if(a->mx!=NULL) free(a->mx);
    a->sz = NULL;
    a->mx = NULL;
    a->n  = a->r  = 0;
}

Here is the caller graph for this function:

int* get_imatrix	(	imatrix	mtx,
			...
	)

int* get_imatrix(imatrix mtx, ...)

Matrix の要素を返す．次元数に制限はない．インデックスは1から数える（0からではない）．

参考：1次元配列へのアクセスインデックス
    1次元: (i)                                                                    (i-1)
    2次元: (i,j)                                        (j-1) +             sz[1]*(i-1)
    3次元: (i,j,k)                  (k-1) +       sz[2]*(j-1) +       sz[1]*sz[2]*(i-1)
    4次元: (i,j,k,l)  (l-1) + sz[3]*(k-1) + sz[2]*sz[3]*(j-1) + sz[1]*sz[2]*sz[3]*(i-1)
    ...................

Definition at line 500 of file matrix.c.

References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

{
    int   m, d;
    int*  args;
    va_list argsptr;
        
    if (mtx.n<1) return NULL;
    args = (int*)malloc(mtx.n*sizeof(int));
    if (args==NULL) return NULL;

    va_start(argsptr, mtx);
    for (m=0; m<mtx.n; m++) {
        args[m] = (int)va_arg(argsptr, int);
    }
    va_end(argsptr);

    int dx = args[0] - 1;
    for (d=1; d<mtx.n; d++) dx = dx*mtx.sz[d] + args[d] - 1;
    free(args);

    if (dx>=mtx.r || dx<0) return NULL;
    return &mtx.mx[dx];
}

double* get_matrix	(	matrix	mtx,
			...
	)

double* get_matrix(matrix mtx, ...)

Matrix の要素を返す．次元数に制限はない．インデックスは1から数える（0からではない）．

参考：1次元配列へのアクセスインデックス
    1次元: (i)                                                                    (i-1)
    2次元: (i,j)                                        (j-1) +             sz[1]*(i-1)
    3次元: (i,j,k)                  (k-1) +       sz[2]*(j-1) +       sz[1]*sz[2]*(i-1)
    4次元: (i,j,k,l)  (l-1) + sz[3]*(k-1) + sz[2]*sz[3]*(j-1) + sz[1]*sz[2]*sz[3]*(i-1)
    ...................

Definition at line 460 of file matrix.c.

References matrix::mx, matrix::n, matrix::r, and matrix::sz.

{
    int   m, d;
    int*  args;
    va_list argsptr;
        
    if (mtx.n<1) return NULL;
    args = (int*)malloc(mtx.n*sizeof(int));
    if (args==NULL) return NULL;

    va_start(argsptr, mtx);
    for (m=0; m<mtx.n; m++) {
        args[m] = (int)va_arg(argsptr, int);
    }
    va_end(argsptr);

    int dx = args[0] - 1;
    for (d=1; d<mtx.n; d++) dx = dx*mtx.sz[d] + args[d] - 1;
    free(args);

    if (dx>=mtx.r || dx<0) return NULL;
    return &mtx.mx[dx];
}

vector i2vector

(

ivector

a

)

vector i2vector(ivector a)

整数ベクトル a から実数ベクトルをつくり出し,それを返す．

Parameters:

a

変換する整数ベクトル．

Returns:

変換された実数ベクトル．

Definition at line 152 of file matrix.c.

References vector::n, ivector::x, vector::x, ivector::y, vector::y, ivector::z, and vector::z.

{
    vector c;

    c.x = (double)a.x;
    c.y = (double)a.y;
    c.z = (double)a.z;
    c.n = sqrt(c.x*c.x + c.y*c.y + c.z*c.z);
    return c;
}

matrix invrU_matrix

(

matrix

x

)

matrix invrU_matrix(matrix x)

2次元の上三角行列 xの逆行列を求める．

Parameters:

x

操作対象行列(上三角行列)．

Returns:

xの逆行列．

Definition at line 1060 of file matrix.c.

References make_matrix(), Mx, matrix::mx, matrix::n, matrix::r, and matrix::sz.

Referenced by minimum2().

{
    int    i, j, k, n;
    double t, u, det;
    matrix a;

    a.n = a.r = 0;
    a.sz = NULL;
    a.mx = NULL;
    if (x.mx==NULL)       return a;
    if (x.sz[0]!=x.sz[1]) return a;

    n = x.sz[0];  // 上三角行列のチェック
    for (j=1; j<n; j++) {
        for (i=j+1; i<=n; i++) {
            if (Mx(x,i,j) != 0.0) return a;
        }
    }
        
    det = 1.0;
    a = make_matrix(x.n, x.sz);
    if (a.mx==NULL) return a;

    for (i=0; i<a.r; i++) a.mx[i] = x.mx[i];

    for (k=1; k<=n; k++) {
        t = Mx(a,k,k);
        det = det*t;
        for (i=1; i<=n; i++) Mx(a,i,k) = Mx(a,i,k)/t; 
           Mx(a,k,k) = 1.0/t;

        for (j=1; j<=n; j++) {
            if (j!=k) {
                u = Mx(a,k,j);
                for (i=1; i<=n; i++) {
                    if (i!=k) Mx(a,i,j) = Mx(a,i,j) - Mx(a,i,k)*u;
                    else      Mx(a,i,j) = - u/t;
                }
            }
        }
    }
    return a;
}

Here is the call graph for this function:

Here is the caller graph for this function:

imatrix make_imatrix	(	int	n,
		int *	sz
	)

imatrix make_imatrix(int n, int* sz)

任意(n)次元の整数マトリックスのバッファ部をつくり出す． 要素自体は 0に初期化される．

Parameters:

	n	マトリックスの次元数．
	sz	sz[0]〜sz[n-1]: 各次元の要素数．

Returns:

作成された整数マトリックス．

Definition at line 380 of file matrix.c.

References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

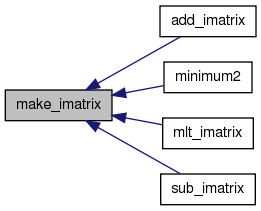
Referenced by add_imatrix(), minimum2(), mlt_imatrix(), and sub_imatrix().

{
    int i, s;
    imatrix a;

    a.n = a.r = 0;
    a.sz = (int*)malloc(n*sizeof(int));
    if (a.sz==NULL) {
        a.mx = NULL;
        return a;
    }
    for (s=1,i=0; i<n; i++) {
        a.sz[i] = sz[i];
        s = s*sz[i];
    }

    a.mx = (int*)malloc(s*sizeof(int));
    if (a.mx==NULL) {
        free(a.sz);
        return a;
    }

    a.n = n;
    a.r = s;
    for (i=0; i<s; i++) a.mx[i] = 0;
    return a;
}

Here is the caller graph for this function:

imatrix make_imatrix1

(

int

n

)

imatrix make_imatrix1(int n)

1次元の整数行列のバッファ部をつくり出す． 要素自体は 0に初期化される．

Parameters:

n

1次元行列の大きさ．

Returns:

作成された1次元整数行列

Definition at line 231 of file matrix.c.

References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

{
    int i;
    imatrix a;

    a.n = a.r = 0;
    a.mx = NULL;
    a.sz = (int*)malloc(sizeof(int));
    if (a.sz==NULL)  return a;
    a.sz[0] = n;

    a.mx = (int*)malloc(n*sizeof(int));
    if (a.mx==NULL) {
        free(a.sz);
        return a;
    }

    a.n = 1;
    a.r = n;
    for (i=0; i<n; i++) a.mx[i] = 0;
    return a;
}

imatrix make_imatrix2	(	int	n,
		int	m
	)

imatrix make_imatrix2(int n, int m)

2次元の整数行列のバッファ部をつくり出す． 要素自体は 0に初期化される．

Parameters:

	n	2次元行列の行の数．
	m	2次元行列の列の数．

Returns:

作成された2次元整数行列

Definition at line 303 of file matrix.c.

References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

{
    int i, s;
    imatrix a;

    a.n = a.r = 0;
    a.mx = NULL;
    a.sz = (int*)malloc(2*sizeof(int));
    if (a.sz==NULL)  return a;
    a.sz[0] = n;
    a.sz[1] = m;
    s = n*m;

    a.mx = (int*)malloc(s*sizeof(int));
    if (a.mx==NULL) {
        free(a.sz);
        return a;
    }

    a.n = 2;
    a.r = s;
    for (i=0; i<s; i++) a.mx[i] = 0;
    return a;
}

matrix make_matrix	(	int	n,
		int *	sz
	)

matrix make_matrix(int n, int* sz)

任意(n)次元の実数マトリックスのバッファ部をつくり出す． 要素自体は 0.0に初期化される．

Parameters:

	n	マトリックスの次元数．
	sz	sz[0]〜sz[n-1]: 各次元の要素数．

Returns:

作成されたマトリックス．

Definition at line 340 of file matrix.c.

References matrix::mx, matrix::n, matrix::r, and matrix::sz.

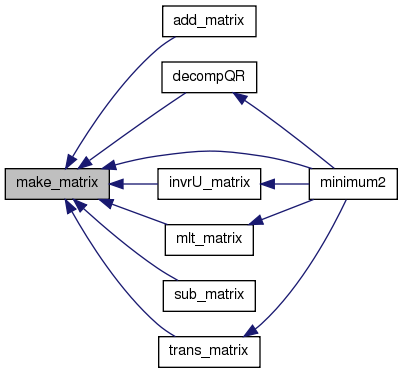
Referenced by add_matrix(), decompQR(), invrU_matrix(), minimum2(), mlt_matrix(), sub_matrix(), and trans_matrix().

{
    int i, s;
    matrix a;

    a.n = a.r = 0;
    a.sz = (int*)malloc(n*sizeof(int));
    if (a.sz==NULL) {
        a.mx = NULL;
        return a;
    }
    for (s=1,i=0; i<n; i++) {
        a.sz[i] = sz[i];
        s = s*sz[i];
    }

    a.mx = (double*)malloc(s*sizeof(double));
    if (a.mx==NULL) {
        free(a.sz);
        return a;
    }

    a.n = n;
    a.r = s;
    for (i=0; i<s; i++) a.mx[i] = 0.0;
    return a;
}

Here is the caller graph for this function:

matrix make_matrix1

(

int

n

)

matrix make_matrix1(int n)

1次元の実数行列のバッファ部をつくり出す． 要素自体は 0.0に初期化される．

Parameters:

n

1次元行列の大きさ．

Returns:

作成された1次元行列

Definition at line 197 of file matrix.c.

References matrix::mx, matrix::n, matrix::r, and matrix::sz.

{
    int i;
    matrix a;

    a.n = a.r = 0;
    a.mx = NULL;
    a.sz = (int*)malloc(sizeof(int));
    if (a.sz==NULL)  return a;
    a.sz[0] = n;

    a.mx = (double*)malloc(n*sizeof(double));
    if (a.mx==NULL) {
        free(a.sz);
        return a;
    }

    a.n = 1;
    a.r = n;
    for (i=0; i<n; i++) a.mx[i] = 0.0;
    return a;
}

matrix make_matrix2	(	int	n,
		int	m
	)

matrix make_matrix2(int n, int m)

2次元の実数行列のバッファ部をつくり出す． 要素自体は 0.0に初期化される．

Parameters:

	n	2次元行列の行の数．
	m	2次元行列の列の数．

Returns:

作成された2次元行列

Definition at line 266 of file matrix.c.

References matrix::mx, matrix::n, matrix::r, and matrix::sz.

{
    int i, s;
    matrix a;

    a.n = a.r = 0;
    a.mx = NULL;
    a.sz = (int*)malloc(2*sizeof(int));
    if (a.sz==NULL)  return a;
    a.sz[0] = n;
    a.sz[1] = m;
    s = n*m;

    a.mx = (double*)malloc(s*sizeof(double));
    if (a.mx==NULL) {
        free(a.sz);
        return a;
    }

    a.n = 2;
    a.r = s;
    for (i=0; i<s; i++) a.mx[i] = 0.0;
    return a;
}

matrix minimum2	(	matrix	y,
		matrix	x
	)

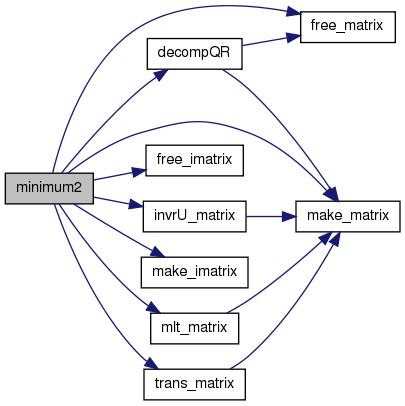
matrix minimum2(matrix y, matrix x)

最小2乗法で方程式の近似解を解き,結果を返す． ただし, x,yは2次元行列のみ．

Parameters:

	y	連立方程式の結果の行列 (例を見よ)
	x	連立方程式の変数の行列 (例を見よ)

Returns:

連立方程式の係数の行列 (例を見よ)

例

以下の場合 A = minimum2(Y, X) で解く(a1,a2を求める)．

Y = X・A   
    y1 = x11*a1 + x12*a2
    y2 = x21*a1 + x22*a2
    y3 = x31*a1 + x32*a2

Definition at line 980 of file matrix.c.

References decompQR(), free_imatrix(), free_matrix(), invrU_matrix(), make_imatrix(), make_matrix(), mlt_matrix(), imatrix::mx, matrix::mx, matrix::n, matrix::r, matrix::sz, and trans_matrix().

{
    int  i, m;
    imatrix cl;
    matrix  rx, rt, rr, aa, bb, cc;
   
    cc.n = cc.r = 0;
    cc.sz = NULL;
    cc.mx = NULL;
    if (y.mx==NULL || x.mx==NULL) return cc;
    if (y.sz[0]!=x.sz[0])         return cc;

    //n  = x.sz[0];
    m  = x.sz[1];       /* n×m 行列 n>=m */
    cl = make_imatrix(1, &m);
    if (cl.mx==NULL) return cc;
    cc = make_matrix (1, &m);
    if (cc.mx==NULL) {free_imatrix(&cl); return cc;}

    rx = decompQR(x, cl);
    rr = invrU_matrix(rx), 
    rt = mlt_matrix(rr, trans_matrix(rr)); 
    aa = mlt_matrix(trans_matrix(x), y), 
    bb = mlt_matrix(rt, aa);

    if (bb.mx!=NULL) for (i=0; i<m; i++) cc.mx[cl.mx[i]-1] = bb.mx[i];

    free_imatrix(&cl);
    free_matrix(&rx);
    free_matrix(&rr);
    free_matrix(&rt);
    free_matrix(&aa);
    free_matrix(&bb);

    return cc;
}

Here is the call graph for this function:

imatrix mlt_imatrix	(	imatrix	a,
		imatrix	b
	)

imatrix mlt_imatrix(imatrix a, imatrix b)

マトリックスのかけ算． 整数マトリックス a, bをかけ算して,結果の整数マトリックスを返す．

Parameters:

	a	かけられるマトリックス．
	b	かけるマトリックス．

Returns:

かけ算結果の整数マトリックス．

Definition at line 765 of file matrix.c.

References make_imatrix(), imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

{
    int  i, j, k, n, ii, aa, bb, st;
    int  *sz, *sa, *sb, *sc, *cx;
    imatrix c;

    c.n = c.r = 0;
    c.sz = NULL;
    c.mx = NULL;
    if (a.mx==NULL || b.mx==NULL) return c;
    if (a.sz[a.n-1]!=b.sz[0])     return c;

    n  = a.n + b.n - 2;
    sz = (int*)malloc(n*sizeof(int));
    if (sz==NULL) return c;
    sa = (int*)malloc(a.n*sizeof(int));
    if (sa==NULL) {free(sz); return c;}
    sb = (int*)malloc(b.n*sizeof(int));
    if (sb==NULL) {free(sz); free(sa); return c;}
    sc = (int*)malloc(n*sizeof(int));
    if (sc==NULL) {free(sz); free(sa); free(sb); return c;}
    cx = (int*)malloc(n*sizeof(int));
    if (cx==NULL) {free(sz); free(sa); free(sb); free(sc); return c;}


    for (i=0; i<a.n-1; i++) sz[i] = a.sz[i];
    for (i=1; i<b.n; i++)   sz[a.n-2+i] = b.sz[i];

    sa[a.n-1] = sb[b.n-1] = sc[n-1] = 1;
    for (i=a.n-2; i>=0; i--) sa[i] = sa[i+1]*a.sz[i+1];
    for (i=b.n-2; i>=0; i--) sb[i] = sb[i+1]*b.sz[i+1];
    for (i=n-2;   i>=0; i--) sc[i] = sc[i+1]*sz[i+1];

    c = make_imatrix(n, sz);

    for (i=0; i<c.r; i++) {
        ii = i;
        for (j=0; j<c.n; j++) {
            cx[j] = ii / sc[j]; 
            ii = ii % sc[j];
        }
        aa = bb = 0;
        for (j=0; j<a.n-1; j++) aa = aa + sa[j]*cx[j]; 
        for (j=1; j<b.n; j++)   bb = bb + sb[j]*cx[j+a.n-2];

        st = 0;
        for (k=0; k<b.sz[0]; k++) st = st + a.mx[k+aa]*b.mx[bb+sb[0]*k];
        c.mx[i] = st;
    }
        
    free(sz);
    free(sa);
    free(sb);
    free(sc);
    free(cx);

    return c;
}

Here is the call graph for this function:

matrix mlt_matrix	(	matrix	a,
		matrix	b
	)

matrix mlt_matrix(matrix a, matrix b)

マトリックスのかけ算． 実数マトリックス a, bをかけ算して,結果の実数マトリックスを返す．

Parameters:

	a	かけられるマトリックス．
	b	かけるマトリックス．

Returns:

かけ算結果のマトリックス．

Definition at line 694 of file matrix.c.

References make_matrix(), matrix::mx, matrix::n, matrix::r, and matrix::sz.

Referenced by minimum2().

{
    int  i, j, k, n, ii, aa, bb;
    int  *sz, *sa, *sb, *sc, *cx;
    double st;
    matrix c;

    c.n = c.r = 0;
    c.sz = NULL;
    c.mx = NULL;
    if (a.mx==NULL || b.mx==NULL) return c;
    if (a.sz[a.n-1]!=b.sz[0])     return c;

    n  = a.n + b.n - 2;
    sz = (int*)malloc(n*sizeof(int));
    if (sz==NULL) return c;
    sa = (int*)malloc(a.n*sizeof(int));
    if (sa==NULL) {free(sz); return c;}
    sb = (int*)malloc(b.n*sizeof(int));
    if (sb==NULL) {free(sz); free(sa); return c;}
    sc = (int*)malloc(n*sizeof(int));
    if (sc==NULL) {free(sz); free(sa); free(sb); return c;}
    cx = (int*)malloc(n*sizeof(int));
    if (cx==NULL) {free(sz); free(sa); free(sb); free(sc); return c;}

    for (i=0; i<a.n-1; i++) sz[i] = a.sz[i];
    for (i=1; i<b.n; i++)   sz[a.n-2+i] = b.sz[i];

    sa[a.n-1] = sb[b.n-1] = sc[n-1] = 1;
    for (i=a.n-2; i>=0; i--) sa[i] = sa[i+1]*a.sz[i+1];
    for (i=b.n-2; i>=0; i--) sb[i] = sb[i+1]*b.sz[i+1];
    for (i=n-2;   i>=0; i--) sc[i] = sc[i+1]*sz[i+1];

    c = make_matrix(n, sz);

    for (i=0; i<c.r; i++) {
        ii = i;
        for (j=0; j<c.n; j++) {
            cx[j] = ii / sc[j]; 
            ii = ii % sc[j];
        }
        aa = bb = 0;
        for (j=0; j<a.n-1; j++) aa = aa + sa[j]*cx[j]; 
        for (j=1; j<b.n; j++)   bb = bb + sb[j]*cx[j+a.n-2];

        st = 0.0;
        for (k=0; k<b.sz[0]; k++) st = st + a.mx[k+aa]*b.mx[bb+sb[0]*k];
        c.mx[i] = st;
    }
        
    free(sz);
    free(sa);
    free(sb);
    free(sc);
    free(cx);

    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void print_imatrix	(	FILE *	fp,
		imatrix	a
	)

void print_imatrix(FILE* fp, imatrix a)

整数マトリックスの要素を標準出力に書き出す．

Parameters:

	fp	出力先のファイル記述子
	a	プリントするマトリックス．

Definition at line 854 of file matrix.c.

References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

{
    int  i;
    for (i=0; i<a.r; i++) {
        fprintf(fp, "  %6d", a.mx[i]);
        if ((i+1)%a.sz[a.n-1]==0) fprintf(fp, "\n");
    }
    fprintf(stdout,"\n");
}

void print_matrix	(	FILE *	fp,
		matrix	a
	)

void print_matrix(FILE* fp, matrix a)

実数マトリックスの要素を標準出力に書き出す．

Parameters:

	fp	出力先のファイル記述子
	a	プリントするマトリックス．

Definition at line 834 of file matrix.c.

References matrix::mx, matrix::n, matrix::r, and matrix::sz.

{
    int  i;
    for (i=0; i<a.r; i++) {
        fprintf(fp, "  %15lf", a.mx[i]);
        if ((i+1)%a.sz[a.n-1]==0) fprintf(fp, "\n");
    }
//    fprintf(stdout,"\n");
}

ivector set_ivector	(	int	x,
		int	y,
		int	z
	)

ivector set_ivector(int x, int y, int z)

整数ベクトルの作成．x方向成分, y方向成分, z方向成分から整数ベクトルを作り,それを返す．

Parameters:

	x	ベクトルの x成分．
	y	ベクトルの y成分．
	z	ベクトルの z成分．

Returns:

作成された整数ベクトル．

Definition at line 109 of file matrix.c.

References ivector::n, ivector::x, ivector::y, and ivector::z.

{
    ivector c;

    c.x = x;
    c.y = y;
    c.z = z;
    c.n = sqrt((double)x*x + y*y + z*z);
    return c;
}

vector set_vector	(	double	x,
		double	y,
		double	z
	)

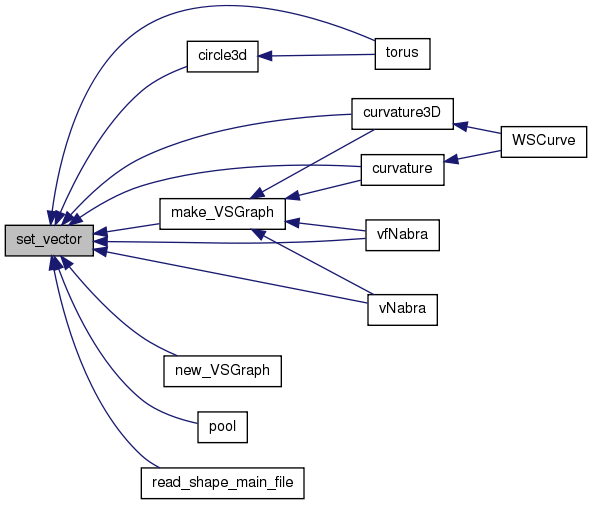
vector set_vector(double x, double y, double z)

ベクトルの作成．x方向成分, y方向成分, z方向成分から実数ベクトルを作り,それを返す．

Parameters:

	x	ベクトルの x成分．
	y	ベクトルの y成分．
	z	ベクトルの z成分．

Returns:

作成されたベクトル．

Definition at line 86 of file matrix.c.

References vector::n, vector::x, vector::y, and vector::z.

Referenced by circle3d(), curvature(), curvature3D(), make_VSGraph(), new_VSGraph(), pool(), read_shape_main_file(), torus(), vfNabra(), and vNabra().

{
    vector c;

    c.x = x;
    c.y = y;
    c.z = z;
    c.n = sqrt(x*x + y*y + z*z);
    return c;
}

Here is the caller graph for this function:

imatrix sub_imatrix	(	imatrix	a,
		imatrix	b
	)

imatrix sub_imatrix(imatrix a, imatrix b)

マトリックスの引き算． 整数マトリックス a, bを引き算して,結果の整数マトリックスを返す．

Parameters:

	a	引かれるマトリックス．
	b	引くマトリックス．

Returns:

引き算結果の整数マトリックス．

Definition at line 666 of file matrix.c.

References make_imatrix(), imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

{
    int  i;
    imatrix c;

    c.n = c.r = 0;
    c.sz = NULL;
    c.mx = NULL;
    if (a.mx==NULL || b.mx==NULL) return c;
    if (a.r != b.r)               return c;

    c = make_imatrix(a.n, a.sz);
    for (i=0; i<c.r; i++) c.mx[i] = a.mx[i] - b.mx[i];
    return c;
}

Here is the call graph for this function:

matrix sub_matrix	(	matrix	a,
		matrix	b
	)

matrix sub_matrix(matrix a, matrix b)

マトリックスの引き算． 実数マトリックス a, bを引き算して,結果の実数マトリックスを返す．

Parameters:

	a	引かれるマトリックス．
	b	引くマトリックス．

Returns:

引き算結果のマトリックス．

Definition at line 638 of file matrix.c.

References make_matrix(), matrix::mx, matrix::n, matrix::r, and matrix::sz.

{
    int  i;
    matrix c;

    c.n = c.r = 0;
    c.sz = NULL;
    c.mx = NULL;
    if (a.mx==NULL || b.mx==NULL) return c;
    if (a.r != b.r)               return c;

    c = make_matrix(a.n, a.sz);
    for (i=0; i<c.r; i++) c.mx[i] = a.mx[i] - b.mx[i];
    return c;
}

Here is the call graph for this function:

matrix trans_matrix

(

matrix

a

)

matrix trans_matrix(matrix a)

2次元行列 aの転置行列を返す．

Parameters:

a

操作対象行列．

Returns:

aの転置行列．

Definition at line 1027 of file matrix.c.

References make_matrix(), matrix::mx, matrix::n, matrix::r, and matrix::sz.

Referenced by minimum2().

{ 
    int    i, j, k;
    matrix c;
    int sz[2]; 

    c.n = c.r = 0;
    c.sz = NULL;
    c.mx = NULL;
    if (a.mx==NULL || a.n!=2) return c; 

    sz[0] = a.sz[1];
    sz[1] = a.sz[0];
    c = make_matrix(a.n, sz); 
 
    for (k=0; k<c.r; k++) {
        i = k/a.sz[1];
        j = k%a.sz[1]; 
        c.mx[j*sz[1]+i] = a.mx[k]; 
   }    
   return c; 
}       

Here is the call graph for this function:

Here is the caller graph for this function:

vector unit_ivector

(

ivector

a

)

vector unit_ivector(ivector a)

整数ベクトル aの単位ベクトルを返す．返されるベクトルは実数ベクトル．

Parameters:

a

対象整数ベクトル．

Returns:

a の単位ベクトル(実数ベクトル)．

Definition at line 52 of file matrix.c.

References EPS, vector::n, vector::x, ivector::x, Xabs, vector::y, ivector::y, vector::z, and ivector::z.

{
    vector c;
    double r;

    r = a.x*a.x+a.y*a.y+a.z*a.z;
    if (Xabs(r)<EPS*EPS) {
        c.x = 0.0;
        c.y = 0.0;
        c.z = 0.0;
        c.n = 1.0;
    }
    else {
        r   = sqrt(r);
        c.x = a.x/r;
        c.y = a.y/r;
        c.z = a.z/r;
        c.n = 1.0;
    }
    return c;
}

vector unit_vector

(

vector

a

)

vector unit_vector(vector a)

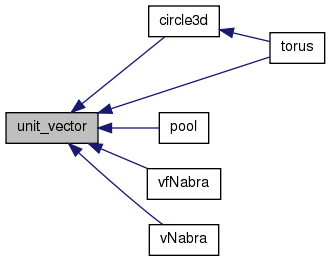
ベクトル aの単位ベクトルを返す．

Parameters:

a

対象ベクトル．

Returns:

a の単位ベクトル．

Definition at line 20 of file matrix.c.

References EPS, vector::n, vector::x, Xabs, vector::y, and vector::z.

Referenced by circle3d(), pool(), torus(), vfNabra(), and vNabra().

{
    vector c;
    double r;

    r = a.x*a.x+a.y*a.y+a.z*a.z;
    if (Xabs(r)<EPS*EPS) {
        c.x = 0.0;
        c.y = 0.0;
        c.z = 0.0;
        c.n = 1.0;
    }
    else {
        r   = sqrt(r);
        c.x = a.x/r;
        c.y = a.y/r;
        c.z = a.z/r;
        c.n = 1.0;
    }
    return c;
}

Here is the caller graph for this function: