Quaternion< T > Class Template Reference

#include <Rotation.h>

Collaboration diagram for Quaternion< T >:

Public Member Functions
	Quaternion (void)
	Quaternion (T S, T X, T Y, T Z, T N=(T) 0.0, T C=(T) 1.0)
	Quaternion (T S, Vector< T > v)
virtual	~Quaternion (void)
T	norm (void)
void	normalize (void)
void	set (T S, T X, T Y, T Z, T N=(T) 0.0, T C=(T) 1.0)
void	init (T C=(T) 1.0)
Vector< T >	getVector ()
T	getScalar ()
T	getAngle ()
	0〜2π
T	getMathAngle ()
	-π〜π
Matrix< T >	getRotMatrix ()
void	setRotation (T e, Vector< T > v)
void	setRotation (T e, T X, T Y, T Z, T N=(T) 0.0)
void	setRotate (T e, Vector< T > v)
void	setRotate (T e, T X, T Y, T Z, T N=(T) 0.0)
void	setExtEulerXYZ (Vector< T > e)
	X->Y->Z.
void	setExtEulerZYX (Vector< T > e)
	Z->Y->X.
void	setExtEulerXZY (Vector< T > e)
	X->Z->Y.
void	setExtEulerYZX (Vector< T > e)
	Y->Z->X.
void	setExtEulerYXZ (Vector< T > e)
	Y->X->Z.
void	setExtEulerZXY (Vector< T > e)
	Z->X->Y.
Vector< T >	getExtEulerXYZ (Vector< T > *vt=NULL)
Vector< T >	getExtEulerZYX (Vector< T > *vt=NULL)
Vector< T >	getExtEulerXZY (Vector< T > *vt=NULL)
Vector< T >	getExtEulerYZX (Vector< T > *vt=NULL)
Vector< T >	getExtEulerYXZ (Vector< T > *vt=NULL)
Vector< T >	getExtEulerZXY (Vector< T > *vt=NULL)
Vector< T >	execRotation (Vector< T > v)
	Exec Rotation qv(~q).
Vector< T >	execInvRotation (Vector< T > v)
	Exec Inv Rotation (~q)vq.
Vector< T >	execRotate (Vector< T > v)
Vector< T >	execInvRotate (Vector< T > v)
Public Attributes
T	s
T	x
T	y
T	z
T	n
	ノルム
T	c
	信頼度

Detailed Description

template<typename T = double>
class jbxl::Quaternion< T >

class DllExport Quaternion

クォータニオンの定義

回転の合成：A*B => Bの回転 -> Aの回転

Definition at line 45 of file Rotation.h.

Constructor & Destructor Documentation

Quaternion ( void ) [inline]

Definition at line 57 of file Rotation.h.

00057 { init();}

Quaternion	(	T	S,
		T	X,
		T	Y,
		T	Z,
		T	N = `(T)0.0`,
		T	C = `(T)1.0`
	)			`[inline]`

Definition at line 58 of file Rotation.h.

00058 { set(S, X, Y, Z, N, C);}

Quaternion	(	T	S,
		Vector< T >	v
	)			`[inline]`

Definition at line 59 of file Rotation.h.

00059 { setRotation(S, v);}

virtual ~Quaternion ( void ) [inline, virtual]

Definition at line 60 of file Rotation.h.

00060 {}

Member Function Documentation

Vector<T> execInvRotate ( Vector< T > v ) [inline]

Definition at line 99 of file Rotation.h.

00099 { return execInvRotation(v);}

Vector< T > execInvRotation ( Vector< T > v ) [inline]

Definition at line 634 of file Rotation.h.

References Quaternion< T >::c, Vector< T >::d, and Quaternion< T >::getVector().

00635 {
00636     if (c<(T)0.0) return v;
00637 
00638     Quaternion<T> inv = ~(*this);
00639     Quaternion<T> qut =  inv*(v*(*this));
00640     Vector<T> vct = qut.getVector();
00641     vct.d = v.d;
00642 
00643     return vct;
00644 }

Here is the call graph for this function:

Vector<T> execRotate ( Vector< T > v ) [inline]

Definition at line 98 of file Rotation.h.

00098 { return execRotation(v);}

Vector< T > execRotation ( Vector< T > v ) [inline]

Definition at line 619 of file Rotation.h.

References Quaternion< T >::c, Vector< T >::d, and Quaternion< T >::getVector().

Referenced by FacetTriData::execRotate().

00620 {
00621     if (c<(T)0.0) return v;
00622 
00623     Quaternion<T> inv = ~(*this);
00624     Quaternion<T> qut =  (*this)*(v*inv);
00625     Vector<T> vct = qut.getVector();
00626     vct.d = v.d;
00627 
00628     return vct;
00629 }

Here is the call graph for this function:

Here is the caller graph for this function:

T getAngle ( ) [inline]

Definition at line 70 of file Rotation.h.

Vector<T> getExtEulerXYZ ( Vector< T > * vt = NULL ) [inline]

Definition at line 89 of file Rotation.h.

00089 { return Quaternion2ExtEulerXYZ<T>(*this, vt);}

Vector<T> getExtEulerXZY ( Vector< T > * vt = NULL ) [inline]

Definition at line 91 of file Rotation.h.

00091 { return Quaternion2ExtEulerXZY<T>(*this, vt);}

Vector<T> getExtEulerYXZ ( Vector< T > * vt = NULL ) [inline]

Definition at line 93 of file Rotation.h.

00093 { return Quaternion2ExtEulerYXZ<T>(*this, vt);}

Vector<T> getExtEulerYZX ( Vector< T > * vt = NULL ) [inline]

Definition at line 92 of file Rotation.h.

00092 { return Quaternion2ExtEulerYZX<T>(*this, vt);}

Vector<T> getExtEulerZXY ( Vector< T > * vt = NULL ) [inline]

Definition at line 94 of file Rotation.h.

00094 { return Quaternion2ExtEulerZXY<T>(*this, vt);}

Vector<T> getExtEulerZYX ( Vector< T > * vt = NULL ) [inline]

Definition at line 90 of file Rotation.h.

00090 { return Quaternion2ExtEulerZYX<T>(*this, vt);}

T getMathAngle ( ) [inline]

Definition at line 71 of file Rotation.h.

Referenced by jbxl::SlerpQuaternion().

Here is the caller graph for this function:

Matrix< T > getRotMatrix ( ) [inline]

ベクトルを回転させる場合の回転行列を求める．座標軸の回転の場合は共役クォータニオンで計算する．

Definition at line 597 of file Rotation.h.

References Matrix< T >::element(), Quaternion< T >::n, Quaternion< T >::normalize(), Quaternion< T >::s, Quaternion< T >::x, Quaternion< T >::y, and Quaternion< T >::z.

Referenced by jbxl::Quaternion2ExtEulerXYZ(), jbxl::Quaternion2ExtEulerXZY(), jbxl::Quaternion2ExtEulerYXZ(), jbxl::Quaternion2ExtEulerYZX(), jbxl::Quaternion2ExtEulerZXY(), and jbxl::Quaternion2ExtEulerZYX().

00598 {
00599     Matrix<T> mtx(2, 3, 3);    // 2次元マトリックス, 3x3
00600 
00601     if (n!=(T)1.0) normalize();
00602 
00603     mtx.element(1, 1) = (T)1.0 - (T)2.0*y*y - (T)2.0*z*z;
00604     mtx.element(1, 2) = (T)2.0*x*y - (T)2.0*s*z;
00605     mtx.element(1, 3) = (T)2.0*x*z + (T)2.0*s*y;
00606     mtx.element(2, 1) = (T)2.0*x*y + (T)2.0*s*z;
00607     mtx.element(2, 2) = (T)1.0 - (T)2.0*x*x - (T)2.0*z*z;
00608     mtx.element(2, 3) = (T)2.0*y*z - (T)2.0*s*x;
00609     mtx.element(3, 1) = (T)2.0*x*z - (T)2.0*s*y;
00610     mtx.element(3, 2) = (T)2.0*y*z + (T)2.0*s*x;
00611     mtx.element(3, 3) = (T)1.0 - (T)2.0*x*x - (T)2.0*y*y;
00612 
00613     return mtx;
00614 }

Here is the call graph for this function:

Here is the caller graph for this function:

T getScalar ( ) [inline]

Definition at line 69 of file Rotation.h.

00069 { return s;}

Vector<T> getVector ( ) [inline]

Definition at line 68 of file Rotation.h.

Referenced by Quaternion< T >::execInvRotation(), Quaternion< T >::execRotation(), and jbxl::SlerpQuaternion().

00068 { Vector<T> v(x, y, z, (T)0.0, c); return v;}

Here is the caller graph for this function:

void init ( T C = (T)1.0 ) [inline]

Definition at line 66 of file Rotation.h.

Referenced by Quaternion< T >::normalize(), and jbxl::operator*().

00066 { s=n=(T)1.0; x=y=z=(T)0.0; c=C;}

Here is the caller graph for this function:

T norm ( void ) [inline]

Definition at line 62 of file Rotation.h.

00062 { n = (T)sqrt(s*s+x*x+y*y+z*z); return n;}

void normalize ( void ) [inline]

Definition at line 432 of file Rotation.h.

References Quaternion< T >::init(), Quaternion< T >::n, Quaternion< T >::s, Quaternion< T >::x, Quaternion< T >::y, Quaternion< T >::z, and jbxl::Zero_Eps.

Referenced by Quaternion< T >::getRotMatrix(), and jbxl::SlerpQuaternion().

00433 {
00434     T nrm = (T)sqrt(s*s + x*x + y*y + z*z);
00435     
00436     if (nrm>=Zero_Eps) {
00437         s  = s/nrm;
00438         x  = x/nrm;
00439         y  = y/nrm;
00440         z  = z/nrm;
00441         n  = (T)1.0;
00442     }
00443     else {
00444         init();
00445     }
00446 }

Here is the call graph for this function:

Here is the caller graph for this function:

void set	(	T	S,
		T	X,
		T	Y,
		T	Z,
		T	N = `(T)0.0`,
		T	C = `(T)1.0`
	)			`[inline]`

Definition at line 416 of file Rotation.h.

References Quaternion< T >::c, Quaternion< T >::n, Quaternion< T >::s, Quaternion< T >::x, Quaternion< T >::y, and Quaternion< T >::z.

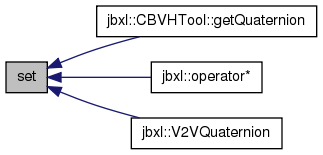
Referenced by CBVHTool::getQuaternion(), jbxl::operator*(), and jbxl::V2VQuaternion().

00417 {
00418     s  = S;
00419     x  = X;
00420     y  = Y;
00421     z  = Z;
00422     n  = N;
00423     c  = C;
00424 
00425     if (n<=0.0) {
00426         n = (T)sqrt(s*s + x*x + y*y + z*z);
00427     }
00428 }

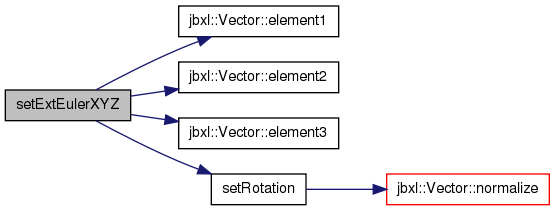
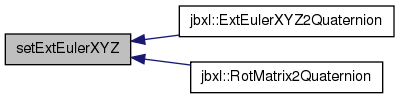
Here is the caller graph for this function:

void setExtEulerXYZ ( Vector< T > e ) [inline]

Definition at line 503 of file Rotation.h.

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), Quaternion< T >::s, and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerXYZ2Quaternion(), and jbxl::RotMatrix2Quaternion().

00504 {
00505     Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
00506     Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
00507     Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
00508 
00509     Quaternion<T> qx, qy, qz;
00510     qx.setRotation(e.element1(), ex);
00511     qy.setRotation(e.element2(), ey);
00512     qz.setRotation(e.element3(), ez);
00513 
00514     (*this) = qz*qy*qx;
00515     if (s<(T)0.0) (*this) = - (*this);
00516 }

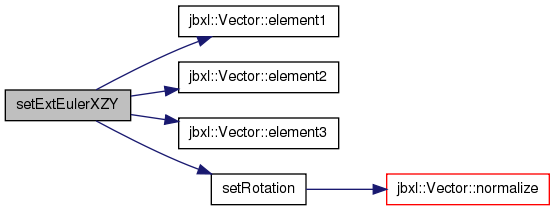
Here is the call graph for this function:

Here is the caller graph for this function:

void setExtEulerXZY ( Vector< T > e ) [inline]

Definition at line 539 of file Rotation.h.

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), Quaternion< T >::s, and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerXZY2Quaternion().

00540 {
00541     Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
00542     Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
00543     Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
00544 
00545     Quaternion<T> qx, qy, qz;
00546     qx.setRotation(e.element1(), ex);
00547     qz.setRotation(e.element2(), ez);
00548     qy.setRotation(e.element3(), ey);
00549 
00550     (*this) = qy*qz*qx;
00551     if (s<(T)0.0) (*this) = - (*this);
00552 }

Here is the call graph for this function:

Here is the caller graph for this function:

void setExtEulerYXZ ( Vector< T > e ) [inline]

Definition at line 557 of file Rotation.h.

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), Quaternion< T >::s, and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerYXZ2Quaternion().

00558 {
00559     Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
00560     Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
00561     Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
00562 
00563     Quaternion<T> qx, qy, qz;
00564     qy.setRotation(e.element1(), ey);
00565     qx.setRotation(e.element2(), ex);
00566     qz.setRotation(e.element3(), ez);
00567 
00568     (*this) = qz*qx*qy;
00569     if (s<(T)0.0) (*this) = - (*this);
00570 }

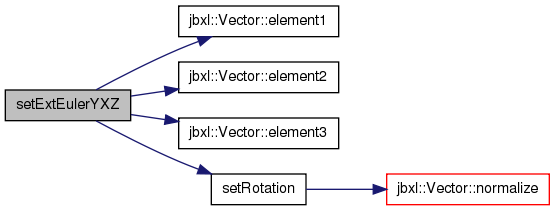
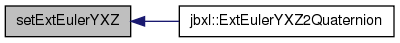
Here is the call graph for this function:

Here is the caller graph for this function:

void setExtEulerYZX ( Vector< T > e ) [inline]

template <typename t>=""> void Quaternion<T>::setExtEulerYZX(Vector<T> e)

Y->Z->X の順にオイラー角でベクトルを回転させる場合のクオータニオンを計算する．

Parameters:

e

オイラー角の成分．作用させる順番に格納する．この場合, e.xはY軸回転，e.yはZ軸回転，e.z はX軸回転のそれぞれの回転角（ラジアン）を格納する．

Definition at line 485 of file Rotation.h.

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), Quaternion< T >::s, and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerYZX2Quaternion().

00486 {
00487     Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
00488     Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
00489     Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
00490 
00491     Quaternion<T> qx, qy, qz;
00492     qy.setRotation(e.element1(), ey);
00493     qz.setRotation(e.element2(), ez);
00494     qx.setRotation(e.element3(), ex);
00495 
00496     (*this) = qx*qz*qy;
00497     if (s<(T)0.0) (*this) = - (*this);
00498 }

Here is the call graph for this function:

Here is the caller graph for this function:

void setExtEulerZXY ( Vector< T > e ) [inline]

Definition at line 575 of file Rotation.h.

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), Quaternion< T >::s, and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerZXY2Quaternion().

00576 {
00577     Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
00578     Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
00579     Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
00580 
00581     Quaternion<T> qx, qy, qz;
00582     qz.setRotation(e.element1(), ez);
00583     qx.setRotation(e.element2(), ex);
00584     qy.setRotation(e.element3(), ey);
00585 
00586     (*this) = qy*qx*qz;
00587     if (s<(T)0.0) (*this) = - (*this);
00588 }

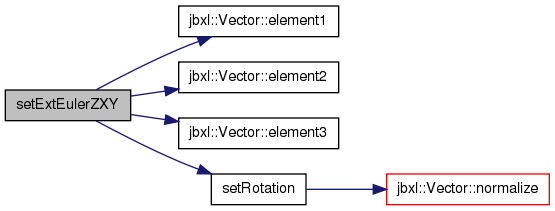
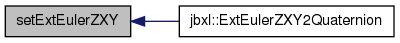
Here is the call graph for this function:

Here is the caller graph for this function:

void setExtEulerZYX ( Vector< T > e ) [inline]

Definition at line 521 of file Rotation.h.

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), Quaternion< T >::s, and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerZYX2Quaternion().

00522 {
00523     Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
00524     Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
00525     Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
00526 
00527     Quaternion<T> qx, qy, qz;
00528     qz.setRotation(e.element1(), ez);
00529     qy.setRotation(e.element2(), ey);
00530     qx.setRotation(e.element3(), ex);
00531 
00532     (*this) = qx*qy*qz;
00533     if (s<(T)0.0) (*this) = - (*this);
00534 }

Here is the call graph for this function:

Here is the caller graph for this function:

void setRotate	(	T	e,
		T	X,
		T	Y,
		T	Z,
		T	N = `(T)0.0`
	)			`[inline]`

Definition at line 79 of file Rotation.h.

00079 { Vector<T> v(X, Y, Z, N); setRotation(e, v);}

void setRotate	(	T	e,
		Vector< T >	v
	)			`[inline]`

Definition at line 78 of file Rotation.h.

00078 { setRotation(e, v);}

void setRotation	(	T	e,
		T	X,
		T	Y,
		T	Z,
		T	N = `(T)0.0`
	)			`[inline]`

Definition at line 76 of file Rotation.h.

Referenced by Quaternion< double >::setRotation().

00076 { Vector<T> v(X, Y, Z, N); setRotation(e, v);}

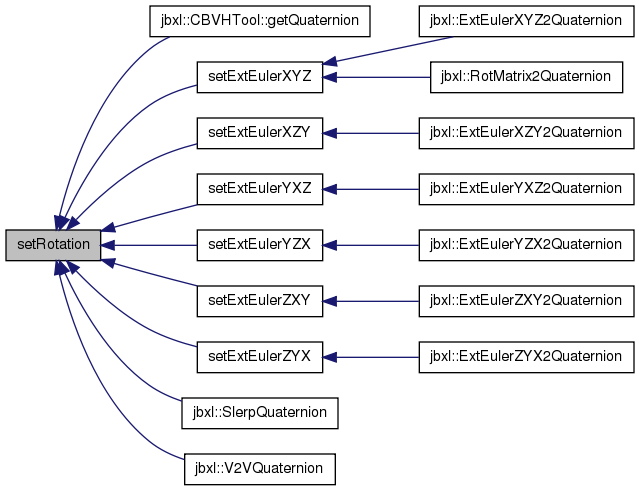
Here is the caller graph for this function:

void setRotation	(	T	e,
		Vector< T >	v
	)			`[inline]`

回転を定義する

Parameters:

	e	回転角．ラジアン単位．
	v	回転軸

Definition at line 456 of file Rotation.h.

References Quaternion< T >::c, Quaternion< T >::n, Vector< T >::n, Vector< T >::normalize(), PI, PI2, Quaternion< T >::s, Vector< T >::x, Quaternion< T >::x, Vector< T >::y, Quaternion< T >::y, Vector< T >::z, and Quaternion< T >::z.

Referenced by CBVHTool::getQuaternion(), Quaternion< T >::setExtEulerXYZ(), Quaternion< T >::setExtEulerXZY(), Quaternion< T >::setExtEulerYXZ(), Quaternion< T >::setExtEulerYZX(), Quaternion< T >::setExtEulerZXY(), Quaternion< T >::setExtEulerZYX(), jbxl::SlerpQuaternion(), and jbxl::V2VQuaternion().

00457 {
00458     if (v.n!=(T)1.0) v.normalize();
00459 
00460     if (e>(T)PI)       e = e - (T)PI2;
00461     else if (e<-(T)PI) e = (T)PI2 + e;
00462 
00463     T s2 = e/(T)2.0;
00464     T sn =(T) sin(s2);
00465     s  = (T)cos(s2);
00466     x  = v.x*sn;
00467     y  = v.y*sn;
00468     z  = v.z*sn;
00469     n  = (T)v.n;
00470     c  = (T)1.0;
00471 }