gLib/graph.h File Reference

2D & 3D グラフィックライブラリ ヘッダ More...

#include "gdata.h"

Include dependency graph for graph.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Defines
#define	set_around_space(vp)   set_around((vp), 0)
#define	SetPixel(vp, x, y, cc)   set_idat((vp), (x), (y), 0, (cc))
#define	GetPixel(vp, x, y)   get_idat((vp), (x), (y), 0)
#define	isCrossLine(x1, y1, x2, y2, x3, y3, x4, y4)   (((x1)-(x2))*((y3)-(y1))+((y1)-(y2))*((x1)-(x3)))*(((x1)-(x2))*((y4)-(y1))+((y1)-(y2))*((x1)-(x4)))
Functions
void	local2world (WSGraph gd, WSGraph vp, vector ox, vector oz, vector ex, double *csf, double *snf)
void	topola (vector nv, double *cst, double *snt, double *csf, double *snf)
void	set_around (WSGraph vp, int cc)
void	bline (BSGraph vp, int xs, int ys, int xe, int ye, int c)
void	bline3d (BSGraph vp, int xs, int ys, int zs, int xe, int ye, int ze, int c)
void	line (WSGraph vp, int xs, int ys, int xe, int ye, int c)
void	line3d (WSGraph vp, int xs, int ys, int zs, int xe, int ye, int ze, int c)
void	circle (WSGraph vp, int x, int y, int r, int c, int mode)
void	paint (WSGraph vp, int x, int y, int mn, int mx, int c, int m)
void	paint3d (WSGraph vp, int x, int y, int z, int mn, int mx, int c, int m)
void	_paint_3d (WSGraph vp, int x, int y, int z, int mn, int mx, int c, int m)
void	box (WSGraph vp, int xs, int ys, int xe, int ye, int c, int m)
void	triangle (WSGraph vp, int x1, int y1, int x2, int y2, int x3, int y3, int c, int m)
void	circle3d (WSGraph vp, vector a, vector b, int rr, int cc, int mode)
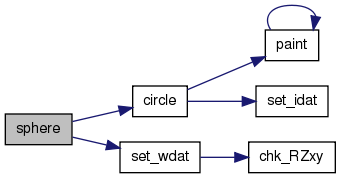
void	sphere (WSGraph vp, vector a, int r, int c, int mode)
void	pool (WSGraph vp, vector a, vector b, int rr, int c)
void	torus (WSGraph vp, vector a, vector b, int rr, int ra, int c)
WSGraph	x_reverse_wsg (WSGraph vp)
WSGraph	cut_object (WSGraph vp, int cc, IRBound *rb, int blank)
WSGraph	zoom_WSGraph (WSGraph vp, int zm, int mode)
WSGraph	grab_WSGraph (WSGraph vp, int x1, int y1, int x2, int y2)
void	copy_WSGraph (WSGraph src, WSGraph dst)
int	get_wdat (WSGraph, double, double, double, IRBound)
int	get_idat (WSGraph, int, int, int)
void	set_wdat (WSGraph, double, double, double, int, IRBound)
void	set_idat (WSGraph, int, int, int, int)
int	get_bdat (BSGraph, int, int, int)
void	set_bdat (BSGraph, int, int, int, int)
int	isinctri (int x1, int y1, int x2, int y2, int x3, int y3, int xx, int yy)

---

Detailed Description

Version:

3.0

Author:

Fumi.Iseki (C)

Definition in file graph.h.

---

Define Documentation

#define GetPixel	(	vp,
		x,
		y		)	get_idat((vp), (x), (y), 0)

int GetPixel(WSGraph vp, int x, int y);

2Dグラフィックデータ構造体 vpの任意の 1pixelの値(濃度)を返す．
座標範囲のチェックあり．

Parameters:

	vp	操作対象となる2Dグラフィックデータ構造体．
	x,y	知りたい値の xy座標．

使用例

    SetPixel(vp, 5, 5, 100);
    SetPixel(vp, 100, 100, 200);
    SetPixel(vp, 100, 200, 10);
    val = GetPixel(vp, 100, 100);  // 当然 val の値は 200

Definition at line 95 of file graph.h.

Referenced by wGetPixel().

#define isCrossLine	(	x1,
		y1,
		x2,
		y2,
		x3,
		y3,
		x4,
		y4		)	(((x1)-(x2))*((y3)-(y1))+((y1)-(y2))*((x1)-(x3)))*(((x1)-(x2))*((y4)-(y1))+((y1)-(y2))*((x1)-(x4)))

int isCrossLine(x1, y1, x2, y2, x3, y3, x4, y4);

(x1,y1)-(x2,y2) の直線と (x3,y3)-(x4,y4) の線分が交差しているか判定する

Return values:

	1以上	交差しない
	0	3か4 は直線上にある
	0未満	交差する

Definition at line 107 of file graph.h.

Referenced by isinctri().

#define set_around_space

(

vp

)

set_around((vp), 0)

Definition at line 55 of file graph.h.

#define SetPixel	(	vp,
		x,
		y,
		cc		)	set_idat((vp), (x), (y), 0, (cc))

void SetPixel(WSGraph vp, int x, int y, int cc)

2Dグラフィックデータ構造体 vpの任意の 1pixelに値を設定する．
座標範囲のチェックあり．

Parameters:

	vp	操作対象となる2Dグラフィックデータ構造体．
	x,y	値を設定する xy座標．
	cc	点(x,y)に設定する点の値(濃度)．

使用例

    SetPixel(vp, 5, 5, 100);      // 座標(5,5)に 100を設定
    SetPixel(vp, 100, 100, 200);  // 座標(100,100)に 200を設定
    SetPixel(vp, 100, 200, 10);   // 座標(100,200)に 10を設定

Definition at line 75 of file graph.h.

Referenced by wSetPixel().

---

Function Documentation

void _paint_3d	(	WSGraph	vp,
		int	x,
		int	y,
		int	z,
		int	mn,
		int	mx,
		int	c,
		int	m
	)

void _paint_3d(WSGraph vp, int x, int y, int z, int mn, int mx, int c, int m)

paint3d() の補助関数

Definition at line 361 of file graph.c.

References _paint_3d(), DEBUG_MODE, WSGraph::gp, paint(), WSGraph::state, WSGraph::xs, WSGraph::ys, and WSGraph::zs.

Referenced by _paint_3d(), and paint3d().

{
    int  i, j, ps, cc;
    WSGraph xp;

    ps  = vp.xs*vp.ys;
    xp.xs = vp.xs;
    xp.ys = vp.ys;
    xp.zs = 1;
    xp.gp = &(vp.gp[z*ps]);
    xp.state = vp.state;

    cc = xp.gp[y*xp.xs+x];
    if (cc>mx || cc<mn) return;
    paint(xp, x, y, mn, mx, c, m);
    if (m<0) {
        DEBUG_MODE fprintf(stderr,"_paint_3d: zz = %d\n",z);
    }

    for (i=0; i<ps; i++) {
        if (xp.gp[i]==c) {
            x = i%vp.xs;
            y = i/vp.xs;
            if (z-1>=0) {
                j = (z-1)*ps+y*vp.xs+x;
                if (vp.gp[j]<=mx && vp.gp[j]>=mn) _paint_3d(vp, x, y, z-1, mn, mx, c, m);
            }
            if (z+1<vp.zs) {
                j = (z+1)*ps+y*vp.xs+x;
                if (vp.gp[j]<=mx && vp.gp[j]>=mn) _paint_3d(vp, x, y, z+1, mn, mx, c, m);
            }
        }
    }

    return;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void bline	(	BSGraph	vp,
		int	x1,
		int	y1,
		int	x2,
		int	y2,
		int	cc
	)

void bline(BSGraph vp, int x1, int y1, int x2, int y2, int cc)

2Dのラインの描画．
点(x1,y1)から点(x2,y2)へ濃度 ccの線を引く．

Parameters:

	vp	操作対象となるグラフィックデータ構造体．
	x1,y1	線の始点の座標．
	x2,y2	線の終点の座標．
	cc	線の濃度．

使用例

line(vp, 100, 200, 300, 300, 200);   // (100,200)から(300,300)へ濃度 200の線を引く 

Definition at line 416 of file graph.c.

References set_bdat().

{
    int  thresh=0, index;
    int  xunit=1;
    int  yunit=1;
    int  xdiff=x2-x1;
    int  ydiff=y2-y1;

    if (xdiff<0) {
        xdiff = -xdiff;
        xunit = -1;
    }
    if (ydiff<0) {
        ydiff = -ydiff;
        yunit = -1;
    }

    if (xdiff>ydiff) {
        for (index=0; index<xdiff+1; index++) {
            set_bdat(vp, x1, y1, 0, cc);
            x1 = x1 + xunit;
            thresh = thresh + ydiff;
            if (thresh>=xdiff) {
                thresh = thresh - xdiff;
                y1 = y1 + yunit;
            }
        }
    }
    else {
        for (index=0; index<ydiff+1; index++) {
            set_bdat(vp, x1, y1, 0, cc);
            y1 = y1 + yunit;
            thresh = thresh + xdiff;
            if (thresh>=ydiff) {
                thresh = thresh - ydiff;
                x1 = x1 + xunit;
            }
        }
    }
}

Here is the call graph for this function:

void bline3d	(	BSGraph	gd,
		int	x1,
		int	y1,
		int	z1,
		int	x2,
		int	y2,
		int	z2,
		int	cc
	)

void bline3d(BSGraph gd, int x1, int y1, int z1, int x2, int y2, int z2, int cc)

3Dのラインの描画．点(x1,y1,z1)から点(x2,y2,z2)へ濃度 ccの線を引く．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	x1,y1,z1	線の始点の座標．
	x2,y2,z2	線の終点の座標．
	cc	線の濃度．

Definition at line 630 of file graph.c.

References set_bdat().

Referenced by draw_shape_polygon().

{
    int  i;
    int  xx, yy, zz, dx, dy, dz;
    int  ux=1, uy=1, uz=1;
    int  sx=0, sy=0, sz=0;

    dx = x2 - x1;
    dy = y2 - y1;
    dz = z2 - z1;

    if (dx<0) {
        dx = -dx;
        ux = -1;
    }
    if (dy<0) {
        dy = -dy;
        uy = -1;
    }
    if (dz<0) {
        dz = -dz;
        uz = -1;
    }

    xx = x1;
    yy = y1;
    zz = z1;

    set_bdat(gd, xx, yy, zz, cc);
    if (dx>=dy && dx>=dz) {
        for (i=1; i<=dx; i++) {
            xx = xx + ux;
            sy = sy + dy;
            sz = sz + dz;
            if (sy>dx) {
                sy = sy - dx;
                yy = yy + uy;
            }
            if (sz>dx) {
                sz = sz - dx;
                zz = zz + uz;
            }
            set_bdat(gd, xx, yy, zz, cc);
        }
    }
    else if (dy>dx && dy>=dz) {
        for (i=1; i<=dy; i++) {
            yy = yy + uy;
            sx = sx + dx;
            sz = sz + dz;
            if (sx>dy) {
                sx = sx - dy;
                xx = xx + ux;
            }
            if (sz>dy) {
                sz = sz - dy;
                zz = zz + uz;
            }
            set_bdat(gd, xx, yy, zz, cc);
        }
    }
    else {
        for (i=1; i<=dz; i++) {
            zz = zz + uz;
            sx = sx + dx;
            sy = sy + dy;
            if (sx>dz) {
                sx = sx - dz;
                xx = xx + ux;
            }
            if (sy>dz) {
                sy = sy - dz;
                yy = yy + uy;
            }
            set_bdat(gd, xx, yy, zz, cc);
        }
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

void box	(	WSGraph	vp,
		int	x1,
		int	y1,
		int	x2,
		int	y2,
		int	cc,
		int	mode
	)

void box(WSGraph vp, int x1, int y1, int x2, int y2, int cc, int mode)

点(x1,y1)-(x2,y2)を対角とした四角形を描く．線の濃度は cc．
modeが 1以上なら，四角形の内部を塗りつぶす．

Parameters:

	vp	操作対象となるグラフィックデータ構造体．
	(x1,y1)-(x2,y2)	四角形の対角の座標．
	cc	線の濃度．
	mode	ON なら四角形の内部の0〜ccをccで塗りつぶす．

使用例

box(vp, 100, 100, 200, 200, 1000, 0);   // (100,100),(200,200)を対角とした四角形を描く 

Definition at line 605 of file graph.c.

References line(), ON, and paint().

{
    line(vp, x1, y1, x2, y1, cc);
    line(vp, x2, y1, x2, y2, cc);
    line(vp, x2, y2, x1, y2, cc);
    line(vp, x1, y2, x1, y1, cc);

    if (mode==ON) {
        paint(vp, (x1+x2)/2, (y1+y2)/2, 0, cc-1, cc, 4); 
    }
    return;
}

Here is the call graph for this function:

void circle	(	WSGraph	gd,
		int	x,
		int	y,
		int	r,
		int	cc,
		int	mode
	)

void circle(WSGraph gd, int x, int y, int r, int cc, int mode)

2Dの円の描画．点(x,y)を中心に半径rで濃度 ccの円を書く．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	x,y	円の中心の座標．
	r	円の半径．
	cc	線の濃度．
	mode	ON なら円の内部の 0〜ccを ccで塗りつぶす．

Definition at line 813 of file graph.c.

References WSGraph::gp, ON, paint(), set_idat(), and WSGraph::xs.

Referenced by circle3d(), pool(), and sphere().

{
    double yy, dy, dt;
    int i, nn, cx;
    int ix, iy, ux=1;
    int *px, *py;

    if (r<=0) return;

    px = (int*)malloc(sizeof(int)*(r+1));
    py = (int*)malloc(sizeof(int)*(r+1));
    if (px==NULL || py==NULL) {
        free(px);
        free(py);
        return;
    }

    ix = 0;
    iy = r;
    yy = (double)r;
    nn = 0;
    px[0] = ix;
    py[0] = iy;

    cx = (y+iy)*gd.xs + (x+ix);
    gd.gp[cx] = cc;
    while(iy>=ix) {
        ix = ix + ux;
        dt = -ux/yy;
        dy = ix*dt;
        yy = yy + dy;
        iy = (int)yy;

        set_idat(gd, x+ix, y+iy, 0, cc);
        nn++;
        px[nn] = ix;
        py[nn] = iy;
    }

    for (i=0; i<=nn; i++) {
        ix = py[nn-i];
        iy = px[nn-i];
        set_idat(gd, x+ix, y+iy, 0, cc);
    }

    for (i=0; i<=nn; i++) {
        ix = py[i];
        iy = -px[i];
        set_idat(gd, x+ix, y+iy, 0, cc);
    }

    for (i=0; i<=nn; i++) {
        ix = px[nn-i];
        iy = -py[nn-i];
        set_idat(gd, x+ix, y+iy, 0, cc);
    }

    for (i=0; i<=nn; i++) {
        ix = -px[i];
        iy = -py[i];
        set_idat(gd, x+ix, y+iy, 0, cc);
    }

    for (i=0; i<=nn; i++) {
        ix = -py[nn-i];
        iy = -px[nn-i];
        set_idat(gd, x+ix, y+iy, 0, cc);
    }

    for (i=0; i<=nn; i++) {
        ix = -py[i];
        iy = px[i];
        set_idat(gd, x+ix, y+iy, 0, cc);
    }

    for (i=0; i<=nn; i++) {
        ix = -px[nn-i];
        iy = py[nn-i];
        set_idat(gd, x+ix, y+iy, 0, cc);
    }

    if (mode==ON) paint(gd, x, y, 0, cc-1, cc, 4);

    free(px);
    free(py);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void circle3d	(	WSGraph	gd,
		vector	ox,
		vector	ex,
		int	rr,
		int	cc,
		int	mode
	)

void circle3d(WSGraph vp, vector ox, vector ex, int rr, int cc, int mode)

3D的な円の描画．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	ox	円の中心の座標ベクトル．
	ex	円の中心の法線ベクトル．
	rr	円の半径．
	cc	線の濃度．
	mode	ON なら円の内部の 0〜ccを ccで塗りつぶす．

Definition at line 914 of file graph.c.

References circle(), WSGraph::gp, local2world(), make_WSGraph(), set_vector(), unit_vector(), WSGraph::xs, and WSGraph::ys.

Referenced by torus().

{
    vector   oz;
    WSGraph  vp;

    vp = make_WSGraph(2*rr+3, 2*rr+3, 1);
    if (vp.gp==NULL) return;
    circle(vp, rr+1, rr+1, rr, cc, mode);

    oz = set_vector((vp.xs-1)/2., (vp.ys-1)/2., 0.0);
    ex = unit_vector(ex);
    local2world(gd, vp, ox, oz, ex, NULL, NULL);

    free(vp.gp);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void copy_WSGraph	(	WSGraph	src,
		WSGraph	dst
	)

void copy_WSGraph(WSGraph src, WSGraph dst)

WSGraph型データのバッファ部をコピーする．とにかくコピーする．できるだけコピーする．

コピー元とコピー先のバッファ部のサイズが合わない場合,コピー結果は保証されない．

Parameters:

	src	コピー元グラフィックデータ
	dst	コピー先グラフィックデータ

Definition at line 1380 of file graph.c.

References WSGraph::gp, Min, WSGraph::xs, WSGraph::ys, and WSGraph::zs.

{
    int  i, ssz, dsz, sz;

    if (src.zs<=0) src.zs = 1;
    if (dst.zs<=0) dst.zs = 1;
    ssz = src.xs*src.ys*src.zs;
    dsz = dst.xs*dst.ys*dst.zs;
    sz  = Min(ssz, dsz);
    
    for (i=0;  i<sz;  i++) dst.gp[i] = src.gp[i];
    for (i=sz; i<dsz; i++) dst.gp[i] = 0;
    return;
}

WSGraph cut_object	(	WSGraph	vp,
		int	cc,
		IRBound *	rb,
		int	blank
	)

WSGraph cut_object(WSGraph vp, int cc, IRBound* rb, int blank)

グラフィックデータから cc以上の輝度値を持つ部分を抜き出す．

Parameters:

	vp	操作対象となるグラフィックデータ構造体．
	cc	抜き出す画像の輝度値．これ以上御輝度値部分を抜き出す．
[out]	rb	指定しない．抜き出された画像の境界情報が入る．
	blank	余白

Returns:

抜き出されたグラフィックデータ．

Definition at line 1174 of file graph.c.

References WSGraph::gp, init_IRBound(), JBXL_GRAPH_MEMORY_ERROR, make_WSGraph(), Max, Min, WSGraph::state, IRBound::xmax, IRBound::xmin, WSGraph::xs, IRBound::ymax, IRBound::ymin, WSGraph::ys, IRBound::zmax, IRBound::zmin, and WSGraph::zs.

{
    int  i, j, k, cx, ax;
    WSGraph xp;

    init_IRBound(rb);

    for (i=0; i<vp.xs; i++) 
    for (j=0; j<vp.ys; j++)
    for (k=0; k<vp.zs; k++) {
        cx = vp.xs*vp.ys*k + vp.xs*j + i;
        if (vp.gp[cx]>=cc) {
            rb->xmax = Max(rb->xmax, i);
            rb->ymax = Max(rb->ymax, j);
            rb->zmax = Max(rb->zmax, k);
            rb->xmin = Min(rb->xmin, i);
            rb->ymin = Min(rb->ymin, j);
            rb->zmin = Min(rb->zmin, k);
        }
    }

    if (blank!=0) {
        rb->xmax += blank;
        rb->ymax += blank;
        rb->zmax += blank;
        rb->xmin -= blank;
        rb->ymin -= blank;
        rb->zmin -= blank;
        rb->xmin = Max(rb->xmin, 0);
        rb->ymin = Max(rb->ymin, 0);
        rb->zmin = Max(rb->zmin, 0);
        rb->zmax = Min(rb->zmax, vp.zs-1);
    }

    xp.xs = rb->xmax - rb->xmin + 1;
    xp.ys = rb->ymax - rb->ymin + 1;
    xp.zs = rb->zmax - rb->zmin + 1;
    xp = make_WSGraph(xp.xs, xp.ys, xp.zs);
    if (xp.gp==NULL) {
        xp.state = JBXL_GRAPH_MEMORY_ERROR;
        return xp;
    }

    for (i=0; i<xp.xs; i++) {
        for (j=0; j<xp.ys; j++) {
            for (k=0; k<xp.zs; k++) {
                cx = xp.xs*xp.ys*k + xp.xs*j + i;
                ax = vp.xs*vp.ys*(k+rb->zmin) + vp.xs*(j+rb->ymin) + (i+rb->xmin);
                if (vp.gp[ax]>=cc) xp.gp[cx] = vp.gp[ax];
            }
        }
    }

    return xp;
}

Here is the call graph for this function:

int get_bdat	(	BSGraph	gd,
		int	xx,
		int	yy,
		int	zz
	)

int get_bdat(BSGraph gd, int xx, int yy, int zz)

グラフィックデータ構造体 vpの任意の 1voxelの値(濃度)を返す．
座標の範囲チェックあり．Z軸の歪補整はなし．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	xx,yy,zz	値を設定する xyz座標．

Returns:

(xx,yy,zz)点の濃度(輝度値)．(xx,yy,zz)が座標の範囲外の場合は0を返す．

Definition at line 79 of file graph.c.

References BSGraph::gp, BSGraph::xs, BSGraph::ys, and BSGraph::zs.

{
    int  ret = 0;

    if (xx>0&&yy>0&&zz>0&&xx<gd.xs&&yy<gd.ys&&zz<gd.zs) {
        ret = (int)gd.gp[zz*gd.xs*gd.ys + yy*gd.xs + xx];
    }
    return  ret;
}

int get_idat	(	WSGraph	gd,
		int	xx,
		int	yy,
		int	zz
	)

int get_idat(WSGraph gd, int xx, int yy, int zz)

グラフィックデータ構造体 vpの任意の 1voxelの値(濃度)を返す．
座標の範囲チェックあり．Z軸の歪補整はなし．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	xx,yy,zz	値を設定する xyz座標．

Returns:

(xx,yy,zz)点の濃度(輝度値)．(xx,yy,zz)が座標の範囲外の場合は0を返す．

Definition at line 25 of file graph.c.

References WSGraph::gp, WSGraph::xs, WSGraph::ys, and WSGraph::zs.

{
    int  ret = 0;

    if (xx>0&&yy>0&&zz>0&&xx<gd.xs&&yy<gd.ys&&zz<gd.zs) {
        ret = gd.gp[zz*gd.xs*gd.ys + yy*gd.xs + xx];
    }
    return  ret;
}

int get_wdat	(	WSGraph	gd,
		double	xx,
		double	yy,
		double	zz,
		IRBound	rb
	)

int get_wdat(WSGraph gd, double xx, double yy, double zz, IRBound rb)

グラフィックデータ構造体 vpの任意の 1voxelの値(濃度)を返す．
座標の範囲チェックあり．Z軸の歪補整あり(RZxy)．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	xx,yy,zz	値を設定する xyz座標．
	rb	境界の底上げ値．rb.?min を基底値にする．

Returns:

(xx,yy,zz)点の濃度(輝度値)．(xx,yy,zz)が座標の範囲外の場合は0を返す．

Definition at line 49 of file graph.c.

References chk_RZxy(), WSGraph::gp, RZxy, IRBound::xmin, WSGraph::xs, IRBound::ymin, WSGraph::ys, IRBound::zmin, and WSGraph::zs.

{
    int  ix, iy, iz;
    int  ret = 0;

    if (chk_RZxy()) zz = zz*RZxy;  // (ex.  *0.4/2.0) 

    ix = (int)(xx+0.5) - rb.xmin;
    iy = (int)(yy+0.5) - rb.ymin;
    iz = (int)(zz+0.5) - rb.zmin;

    if (ix>=0&&ix<gd.xs&&iy>=0&&iy<gd.ys&&iz>=0&&iz<gd.zs){ 
        ret = gd.gp[iz*gd.xs*gd.ys + iy*gd.xs + ix];
    }
    return ret;
}

Here is the call graph for this function:

WSGraph grab_WSGraph	(	WSGraph	vp,
		int	x1,
		int	y1,
		int	x2,
		int	y2
	)

WSGraph grab_WSGraph(WSGraph vp, int x1, int y1, int x2, int y2)

WSGraph型データの (x1,y1)-(x2,y2)の矩形部分だけを取り出す．

(x1,y1)-(x2,y2)が元のデータのサイズを越える場合は,元のデータに合わせられる．

Parameters:

	vp	操作対象グラフィックデータ
	(x1,y1),(x2,y2)	矩形の対角の座標．

Returns:

取り出したグラフィックデータ．

Definition at line 1338 of file graph.c.

References WSGraph::gp, JBXL_GRAPH_MEMORY_ERROR, make_WSGraph(), Max, Min, Px, WSGraph::state, WSGraph::xs, and WSGraph::ys.

{
    int  i, j, xs, xe, ys, ye, xsize, ysize;
    WSGraph xp;

    xs = Min(x1, x2);
    xe = Max(x1, x2);
    xe = Min(xe, vp.xs-1);
    ys = Min(y1, y2);
    ye = Max(y1, y2);
    ye = Min(ye, vp.ys-1);
    xsize = xe - xs + 1;
    ysize = ye - ys + 1;

    xp = make_WSGraph(xsize, ysize, 1);
    if (xp.gp==NULL) {
        memset(&xp, 0, sizeof(WSGraph));
        xp.state = JBXL_GRAPH_MEMORY_ERROR;
        return xp;
    }

    for (j=0; j<ysize; j++) {
        for (i=0; i<xsize; i++) {
            Px(xp, i, j) = Px(vp, i+xs, j+ys);
        }
    }

    return xp;
}

Here is the call graph for this function:

int isinctri	(	int	x1,
		int	y1,
		int	x2,
		int	y2,
		int	x3,
		int	y3,
		int	xx,
		int	yy
	)

int isinctri(int x1, int y1, int x2, int y2, int x3, int y3, int xx, int yy)

点(xx, yy) が三角形の中に含まれているか判定する

Return values:

	TRUE	(xx,yy) は三角形 (x1,y1)-(x2,y2)-(x3,y3)の内部にある．
	FALSE	(xx,yy) は三角形 (x1,y1)-(x2,y2)-(x3,y3)の内部にない．

Definition at line 574 of file graph.c.

References FALSE, isCrossLine, and TRUE.

Referenced by triangle().

{
    int cx, cy;

    cx = (x1 + x2 + x3)/3;
    cy = (y1 + y2 + y3)/3;

    if (isCrossLine(x1, y1, x2, y2, xx, yy, cx, cy)<0) return FALSE;
    if (isCrossLine(x1, y1, x3, y3, xx, yy, cx, cy)<0) return FALSE;
    if (isCrossLine(x2, y2, x3, y3, xx, yy, cx, cy)<0) return FALSE;
    return TRUE;
}

Here is the caller graph for this function:

void line	(	WSGraph	vp,
		int	x1,
		int	y1,
		int	x2,
		int	y2,
		int	cc
	)

void line(WSGraph vp, int x1, int y1, int x2, int y2, int cc)

2Dのラインの描画．
点(x1,y1)から点(x2,y2)へ濃度 ccの線を引く．

Parameters:

	vp	操作対象となるグラフィックデータ構造体．
	x1,y1	線の始点の座標．
	x2,y2	線の終点の座標．
	cc	線の濃度．

使用例

line(vp, 100, 200, 300, 300, 200);   // (100,200)から(300,300)へ濃度 200の線を引く 

Definition at line 475 of file graph.c.

References set_idat().

Referenced by box(), bvh_get_seq_data(), count_lines(), get_tList_line_Buffer(), get_tList_seq_data_Buffer(), triangle(), and wLine().

{
    int  thresh=0, index;
    int  xunit=1;
    int  yunit=1;
    int  xdiff=x2-x1;
    int  ydiff=y2-y1;

    if (xdiff<0) {
        xdiff = -xdiff;
        xunit = -1;
    }
    if (ydiff<0) {
        ydiff = -ydiff;
        yunit = -1;
    }

    if (xdiff>ydiff) {
        for (index=0; index<xdiff+1; index++) {
            set_idat(vp, x1, y1, 0, cc);
            x1 = x1 + xunit;
            thresh = thresh + ydiff;
            if (thresh>=xdiff) {
                thresh = thresh - xdiff;
                y1 = y1 + yunit;
            }
        }
    }
    else {
        for (index=0; index<ydiff+1; index++) {
            set_idat(vp, x1, y1, 0, cc);
            y1 = y1 + yunit;
            thresh = thresh + xdiff;
            if (thresh>=ydiff) {
                thresh = thresh - ydiff;
                x1 = x1 + xunit;
            }
        }
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

void line3d	(	WSGraph	gd,
		int	x1,
		int	y1,
		int	z1,
		int	x2,
		int	y2,
		int	z2,
		int	cc
	)

void line3d(WSGraph gd, int x1, int y1, int z1, int x2, int y2, int z2, int cc)

3Dのラインの描画．点(x1,y1,z1)から点(x2,y2,z2)へ濃度 ccの線を引く．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	x1,y1,z1	線の始点の座標．
	x2,y2,z2	線の終点の座標．
	cc	線の濃度．

Definition at line 721 of file graph.c.

References set_idat().

{
    int  i;
    int  xx, yy, zz, dx, dy, dz;
    int  ux=1, uy=1, uz=1;
    int  sx=0, sy=0, sz=0;

    dx = x2 - x1;
    dy = y2 - y1;
    dz = z2 - z1;

    if (dx<0) {
        dx = -dx;
        ux = -1;
    }
    if (dy<0) {
        dy = -dy;
        uy = -1;
    }
    if (dz<0) {
        dz = -dz;
        uz = -1;
    }

    xx = x1;
    yy = y1;
    zz = z1;

    set_idat(gd, xx, yy, zz, cc);
    if (dx>=dy && dx>=dz) {
        for (i=1; i<=dx; i++) {
            xx = xx + ux;
            sy = sy + dy;
            sz = sz + dz;
            if (sy>dx) {
                sy = sy - dx;
                yy = yy + uy;
            }
            if (sz>dx) {
                sz = sz - dx;
                zz = zz + uz;
            }
            set_idat(gd, xx, yy, zz, cc);
        }
    }
    else if (dy>dx && dy>=dz) {
        for (i=1; i<=dy; i++) {
            yy = yy + uy;
            sx = sx + dx;
            sz = sz + dz;
            if (sx>dy) {
                sx = sx - dy;
                xx = xx + ux;
            }
            if (sz>dy) {
                sz = sz - dy;
                zz = zz + uz;
            }
            set_idat(gd, xx, yy, zz, cc);
        }
    }
    else {
        for (i=1; i<=dz; i++) {
            zz = zz + uz;
            sx = sx + dx;
            sy = sy + dy;
            if (sx>dz) {
                sx = sx - dz;
                xx = xx + ux;
            }
            if (sy>dz) {
                sy = sy - dz;
                yy = yy + uy;
            }
            set_idat(gd, xx, yy, zz, cc);
        }
    }
}

Here is the call graph for this function:

void local2world	(	WSGraph	gd,
		WSGraph	vp,
		vector	ox,
		vector	oz,
		vector	ex,
		double *	pcsf,
		double *	psnf
	)

void local2world(WSGraph gd, WSGraph vp, vector ox, vector oz, vector ex, double* pcsf, double* psnf)

ロカール座標系のグラフィック vpをグローバル座標系のグラフィック gdに埋めこむ．

Parameters:

	gd	グローバル座標系のグラフィックデータ構造体．
	vp	ローカル座標系のグラフィックデータ構造体．
	ox	gdvpの原点の座標．
	oz	gdから見た vpの原点の座標．
	ex	gdから見た vpの座標の向き．
[in,out]	pcsf	通常は cosφの値が入る． sinθが0に近い場合は計算しないので，連続計算の場合は予め直前の cosφの値を入れて置く．
[in,out]	psnf	通常は sinφの値が入る． sinθが0に近い場合は計算しないので，連続計算の場合は予め直前の sinφの値を入れて置く．

Definition at line 197 of file graph.c.

References WSGraph::gp, IRBound::misc, ON, set_wdat(), topola(), vector::x, IRBound::xmin, WSGraph::xs, vector::y, IRBound::ymin, WSGraph::ys, vector::z, IRBound::zmin, and WSGraph::zs.

Referenced by circle3d(), pool(), and torus().

{
    int  x, y, z, cx, cy, cz;
    double px, py, pz, xx, yy, zz;
    double cst, snt, csf=0.0, snf=1.0;
    IRBound rb;

    if (pcsf!=NULL && psnf!=NULL) {
        csf = *pcsf;
        snf = *psnf;
    }

    rb.xmin = rb.ymin = rb.zmin = 0;
    rb.misc = ON;
    topola(ex, &cst, &snt, &csf, &snf);

    for(z=0; z<vp.zs; z++) {
        cz = z*vp.xs*vp.ys;
        for(y=0; y<vp.ys; y++) {
            cy = cz + y*vp.xs;
            for(x=0; x<vp.xs; x++) {
                cx = cy + x;
                if(vp.gp[cx]!=0) {
                    px = z - oz.z;
                    py = oz.x - x;
                    pz = oz.y - y;
                    xx = px*snt*csf - py*snf - pz*cst*csf + ox.x;
                    yy = px*snt*snf + py*csf - pz*cst*snf + ox.y;
                    zz = px*cst              + pz*snt     + ox.z;
                    set_wdat(gd, xx, yy, zz, vp.gp[cx], rb);
                }
            }
        }
    }

    if (pcsf!=NULL && psnf!=NULL) {
        *pcsf = csf;
        *psnf = snf;
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

void paint	(	WSGraph	vp,
		int	x,
		int	y,
		int	mn,
		int	mx,
		int	c,
		int	m
	)

void paint(WSGraph vp, int x, int y, int mn, int mx, int c, int m)

2Dグラフィックの塗りつぶし．
2Dグラフィック vpの点(x,y)から始めて, mn〜mx の輝度値を c で塗りつぶす．

Parameters:

	vp	グラフィックデータ構造体．
	x	塗りつぶしを始める点の x座標．
	y	塗りつぶしを始める点の y座標．
	mn	塗りつぶされる輝度値の最小値
	mx	塗りつぶされる輝度値の最大値．
	c	塗りつぶしの輝度値．
	m	モード 8: 8近傍の塗りつぶし その他: 4近傍の塗りつぶし

Definition at line 256 of file graph.c.

References WSGraph::gp, paint(), Xabs, WSGraph::xs, and WSGraph::ys.

Referenced by _paint_3d(), box(), circle(), and paint().

{
    int  i, j, k, cc;

    if (c<=mx && c>=mn) {
        fprintf(stderr,"PAINT: c = %d. Not be %d< c <%d\n\n",c,mn,mx); 
        return;
    }

    cc = vp.gp[y*vp.xs+x];
    if (cc>mx || cc<mn) return;

    while(x>0) {
        if (vp.gp[y*vp.xs+x-1]>mx || vp.gp[y*vp.xs+x-1]<mn) break;
        x--; 
    }
    k = x;

    while(k<vp.xs) {
        if (vp.gp[y*vp.xs+k]>mx || vp.gp[y*vp.xs+k]<mn) break;
        vp.gp[y*vp.xs+k] = c; 
        k++;
    }
    k--;

    for (i=x; i<=k; i++){ 
        if (y-1>=0 && y-1<vp.ys){ 
            j = (y-1)*vp.xs+i;
            if (vp.gp[j]<=mx && vp.gp[j]>=mn) {
                paint(vp, i, y-1, mn, mx, c, m);
            }

            if (Xabs(m)==8) {  // 8-neighborhood *
                if (i-1>=0) {
                    if (vp.gp[j-1]<=mx && vp.gp[j-1]>=mn) {
                        paint(vp, i-1, y-1, mn, mx, c, m);
                    }
                }
                if (i+1<vp.xs) {
                    if (vp.gp[j+1]<=mx && vp.gp[j+1]>=mn) {
                        paint(vp, i+1, y-1, mn, mx, c, m);
                    }
                }
            }
        }

        if (y+1>=0 && y+1<vp.ys){
            j = (y+1)*vp.xs+i;
            if (vp.gp[j]<=mx && vp.gp[j]>=mn) {
                paint(vp, i, y+1, mn, mx, c, m);
            }

            if (Xabs(m)==8) {  // 8-neighborhood 
                if (i-1>=0) {
                    if (vp.gp[j-1]<=mx && vp.gp[j-1]>=mn) {
                        paint(vp, i-1, y+1, mn, mx, c, m);
                    }
                }
                if (i+1<vp.xs) {
                    if (vp.gp[j+1]<=mx && vp.gp[j+1]>=mn) {
                        paint(vp, i+1, y+1, mn, mx, c, m);
                    }
                }
            }
        }
    }
    return;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void paint3d	(	WSGraph	vp,
		int	x,
		int	y,
		int	z,
		int	mn,
		int	mx,
		int	c,
		int	m
	)

void paint3d(WSGraph vp, int x, int y, int z, int mn, int mx, int c, int m)

3Dグラフィックの塗りつぶし．
3Dグラフィック vpの点(x,y,z)から始めて, mn〜mx の輝度値を c で塗りつぶす．

Parameters:

	vp	グラフィックデータ構造体．
	x,y,z	塗りつぶしを始める点の座標．
	mn	塗りつぶされる輝度値の最小値
	mx	塗りつぶされる輝度値の最大値．
	c	塗りつぶしの輝度値．
	m	モード．マイナスの場合は途中経過を表示． +-8: 8近傍の塗りつぶし その他: 4近傍の塗りつぶし

注：プログラム中で EGMAX を使用．

Definition at line 344 of file graph.c.

References _paint_3d(), WSGraph::gp, SWORDMAX, WSGraph::xs, WSGraph::ys, and WSGraph::zs.

{
    int  i;
 
    _paint_3d(vp, x, y, z, mn, mx, SWORDMAX, m);
    for (i=0; i<vp.xs*vp.ys*vp.zs; i++) {
        if (vp.gp[i]==SWORDMAX) vp.gp[i] = c;
    }
}

Here is the call graph for this function:

void pool	(	WSGraph	gd,
		vector	a,
		vector	b,
		int	rr,
		int	cc
	)

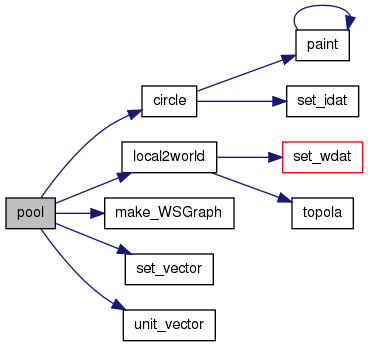
void pool(WSGraph gd, vector a, vector b, int rr, int cc)

3D的な円柱の描画．中身はccで塗りつぶされる．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	a	円柱の一方の底面の円の中心の座標ベクトル．
	b	円柱のもう一方の底面の円の中心の座標ベクトル．
	rr	円柱の半径．
	cc	線と塗りつぶしの濃度．

Definition at line 943 of file graph.c.

References circle(), WSGraph::gp, local2world(), make_WSGraph(), vector::n, ON, set_vector(), sub_vector, unit_vector(), WSGraph::xs, WSGraph::ys, and WSGraph::zs.

{
    int  i, ll, cz;
    vector  ox, oz, ev;
    WSGraph vp, px;

    ox = sub_vector(b, a);
    ll = (int)(ox.n + 0.5);
    vp = px = make_WSGraph(2*rr+3, 2*rr+3, ll);
    if (vp.gp==NULL) return;

    for (i=0; i<vp.zs; i++) {
        cz = i*vp.xs*vp.ys;
        px.gp = &(vp.gp[cz]);
        circle(px, rr+1, rr+1, rr, cc, ON);
    }
    
    oz = set_vector((vp.xs-1)/2., (vp.ys-1)/2., 0.);
    ev = unit_vector(ox);
    local2world(gd, vp, a, oz, ev, NULL, NULL);
    free(vp.gp);

    return;
}

Here is the call graph for this function:

void set_around	(	WSGraph	vp,
		int	cc
	)

void set_around(WSGraph vp, int cc)

2Dグラフィックデータの縁の部分の輝度値を ccにする．

Parameters:

	vp	操作対象となるグラフィックデータ構造体．
	cc	データの縁に設定する輝度値．

Definition at line 1240 of file graph.c.

References WSGraph::gp, WSGraph::xs, and WSGraph::ys.

{
    int  i, px1, px2;

    for (i=0; i<vp.xs; i++){
        px1 = i;
        px2 = (vp.ys-1)*vp.xs + i;
        vp.gp[px1] = cc;
        vp.gp[px2] = cc;
    }
    for (i=1; i<vp.ys-1; i++){
        px1 = vp.xs*i;
        px2 = vp.xs*(i+1) - 1;
        vp.gp[px1] = cc;
        vp.gp[px2] = cc;
    }
}

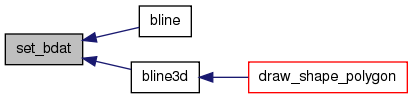
void set_bdat	(	BSGraph	gd,
		int	ix,
		int	iy,
		int	iz,
		int	cc
	)

void set_bdat(BSGraph gd, int ix, int iy, int iz, int cc)

グラフィックデータ構造体 gdの任意の 1voxelに値を設定する．
座標の範囲チェックあり．Z軸の歪補整はなし．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	ix,iy,iz	値を設定する xyz座標．
	cc	点(ix,iy,iz)に設定する点の値(濃度)．

Definition at line 173 of file graph.c.

References BSGraph::gp, BSGraph::xs, BSGraph::ys, and BSGraph::zs.

Referenced by bline(), and bline3d().

{
    if (ix>=0&&ix<gd.xs&&iy>=0&&iy<gd.ys&&iz>=0&&iz<gd.zs){
        gd.gp[iz*gd.xs*gd.ys + iy*gd.xs + ix] = cc;
    }
}

Here is the caller graph for this function:

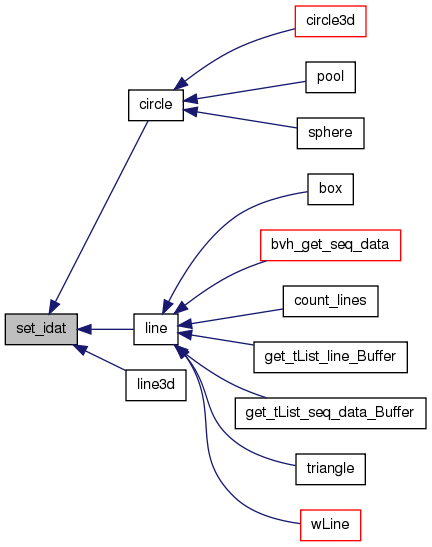
void set_idat	(	WSGraph	gd,
		int	ix,
		int	iy,
		int	iz,
		int	cc
	)

void set_idat(WSGraph gd, int ix, int iy, int iz, int cc)

グラフィックデータ構造体 gdの任意の 1voxelに値を設定する．@ 座標の範囲チェックあり．Z軸の歪補整はなし．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	ix,iy,iz	値を設定する xyz座標．
	cc	点(ix,iy,iz)に設定する点の値(濃度)．

Definition at line 101 of file graph.c.

References WSGraph::gp, WSGraph::xs, WSGraph::ys, and WSGraph::zs.

Referenced by circle(), line(), and line3d().

{
    if (ix>=0&&ix<gd.xs&&iy>=0&&iy<gd.ys&&iz>=0&&iz<gd.zs){
        gd.gp[iz*gd.xs*gd.ys + iy*gd.xs + ix] = cc;
    }
}

Here is the caller graph for this function:

void set_wdat	(	WSGraph	gd,
		double	xx,
		double	yy,
		double	zz,
		int	cc,
		IRBound	rb
	)

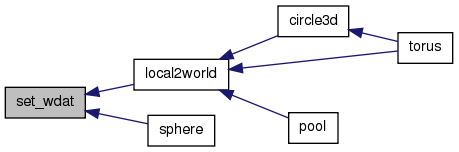
void set_wdat(WSGraph gd, double xx, double yy, double zz, int cc, IRBound rb)

グラフィックデータ構造体 gdの任意の 1voxelに値を設定する．
座標の範囲チェックあり．Z軸の歪補整あり(RZxy)．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	xx,yy,zz	値を設定する xyz座標．
	cc	点(xx,yy,zz)に設定する点の値(濃度)．
	rb	境界の底上げ値．rb.?min を基底値にする． rb.miscが OFの場合，(xx,yy,zz)に一番近い点に ccを設定する． rb.miscが ONの場合，(xx,yy,zz)の周りの 格子点全てに ccを設定する．

Definition at line 123 of file graph.c.

References chk_RZxy(), WSGraph::gp, IRBound::misc, OFF, RZxy, IRBound::xmin, WSGraph::xs, IRBound::ymin, WSGraph::ys, IRBound::zmin, and WSGraph::zs.

Referenced by local2world(), and sphere().

{
    int  i, j, k;
    int  x, y, z;
    int  ix, iy, iz;

    if (chk_RZxy()) zz = zz*RZxy;  // (ex.  *0.4/2.0) 

    if (rb.misc==OFF) {
        ix = (int)(xx+0.5) - rb.xmin;
        iy = (int)(yy+0.5) - rb.ymin;
        iz = (int)(zz+0.5) - rb.zmin;

        if (ix>=0&&ix<gd.xs&&iy>=0&&iy<gd.ys&&iz>=0&&iz<gd.zs){
            gd.gp[iz*gd.xs*gd.ys + iy*gd.xs + ix] = cc;
        }
    }
    else {
        x = (int)(xx) - rb.xmin;
        y = (int)(yy) - rb.ymin;
        z = (int)(zz) - rb.zmin;

        for (i=0; i<=1; i++) {
            for (j=0; j<=1; j++) {
                for (k=0; k<=1; k++) {
                    ix = i + x;
                    iy = j + y;
                    iz = k + z;
                    if (ix>=0&&ix<gd.xs&&iy>=0&&iy<gd.ys&&iz>=0&&iz<gd.zs){
                        gd.gp[iz*gd.xs*gd.ys + iy*gd.xs + ix] = cc;
                    }
                }
            }
        }
    }
    return;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void sphere	(	WSGraph	vp,
		vector	a,
		int	r,
		int	cc,
		int	mode
	)

void sphere(WSGraph vp, vector a, int r, int cc, int mode)

球の描画．

Parameters:

	vp	操作対象となるグラフィックデータ構造体．
	a	球の中心の座標ベクトル．
	r	球の半径．
	cc	線と塗りつぶしの濃度(mode=1のとき)
	mode	モード． 1: 円を重ねて球を作る．中身はccで塗りつぶされる． -1: 極座標で球を作る．vpとの境界に壁を作る． それ以外: 極座標で球を作る．

Definition at line 1029 of file graph.c.

References circle(), WSGraph::gp, IRBound::misc, OFF, ON, PI, RZxy, set_wdat(), vector::x, IRBound::xmin, WSGraph::xs, vector::y, IRBound::ymin, WSGraph::ys, vector::z, IRBound::zmin, and WSGraph::zs.

{
    int i, j, k, rx, nn, s = 1;
    double th, fi, cs, sn, cf, sf, dt;
    double xx, yy, zz, zc;
    WSGraph xp;
    IRBound rb;
 
    memset(&xp, 0, sizeof(WSGraph));

    if (mode==1) {
        xp.xs = vp.xs;
        xp.ys = vp.ys;
        xp.zs = 1;

        for (k=(int)(a.z-r+0.5); k<=(int)(a.z+r+0.5); k++) {
            if (k>=0 && k<vp.zs) {
                xp.gp = &vp.gp[k*vp.xs*vp.ys];
                rx = (int)(sqrt(r*r-(a.z-k)*(a.z-k))+0.5);
                circle(xp, (int)a.x, (int)a.y, rx, cc, ON);
            }
        }   
    }
    else {
        rb.xmin = rb.ymin = rb.zmin = 0;
        rb.misc = OFF;

        nn = (int)(2*PI*r + 0.5)*2;
        dt = PI/nn;
        for (i=0; i<=nn; i++) {
            th = dt*i;
            sn = sin(th);
            cs = cos(th);
            zz = r*cs + a.z;
            zc = zz*RZxy;
            if (mode==-1) {
                if (zc<s)        zz = s/RZxy;
                if (zc>vp.zs-s-1) zz = (vp.zs-s-1)/RZxy;
            }
            for (j=0; j<=2*nn; j++) {
                fi = dt*j;
                cf = cos(fi);
                sf = sin(fi);
                xx = r*sn*cf + a.x;
                yy = r*sn*sf + a.y;
                if (mode==-1) {
                    if (xx<s)         xx = (double)s;
                    if (yy<s)         yy = (double)s;
                    if (xx>vp.xs-s-1) xx = (double)(vp.xs-s-1);
                    if (yy>vp.ys-s-1) yy = (double)(vp.ys-s-1);
                }
                set_wdat(vp, xx, yy, zz, cc, rb);
            }
        }
    }
    return;
}

Here is the call graph for this function:

void topola	(	vector	nv,
		double *	cst,
		double *	snt,
		double *	csf,
		double *	snf
	)

void topola(vector nv, double* cst, double* snt, double* csf, double* snf)

ベクトル nvの単位ベクトルを極座標 (1,θ,φ) へ変換する． ただし，θφは sin, cosの値として返される．

Parameters:

	nv	方向ベクトル．
[out]	cst	指定しない．cosθの値が入る．
[out]	snt	指定しない．sinθの値が入る．
[in,out]	csf	通常は cosφの値が入る． sinθが0に近い場合は計算しないので，連続計算の場合は予め直前の cosφの値を入れて置く．
[in,out]	snf	通常は sinφの値が入る． sinθが0に近い場合は計算しないので，連続計算の場合は予め直前の sinφの値を入れて置く．

Definition at line 1134 of file graph.c.

References EPS, vector::n, Sign, vector::x, vector::y, and vector::z.

Referenced by local2world().

{
    if (nv.n>EPS && nv.n!=1.0) {
        nv.x = nv.x/nv.n;
        nv.y = nv.y/nv.n;
        nv.z = nv.z/nv.n;
    }

    if (nv.z<-1.0) nv.z = -1.0;
    if (nv.z> 1.0) nv.z =  1.0;
    *cst = nv.z;
    *snt = sqrt(1.0-nv.z*nv.z);

    if (*snt<EPS) {
        *cst = Sign(*cst);
        *snt = 0.0;
        //*csf = 0.0;
        //*snf = 1.0;
    }
    else {
        *csf = nv.x / *snt;
        *snf = nv.y / *snt;
    }
    return;
}

Here is the caller graph for this function:

void torus	(	WSGraph	gd,
		vector	ox,
		vector	ex,
		int	rr,
		int	ra,
		int	cc
	)

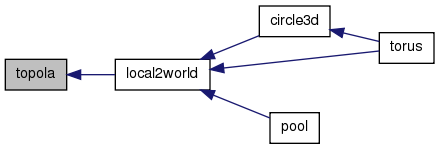
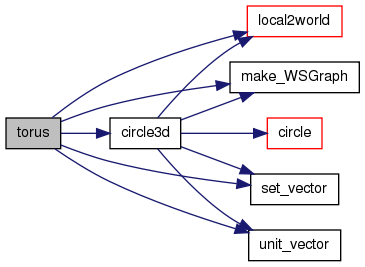
void torus(WSGraph gd, vector ox, vector ex, int rr, int ra, int cc)

3D的なトーラスの描画．中身はccで塗りつぶされる．

Parameters:

	gd	操作対象となるグラフィックデータ構造体．
	ox	トーラスの中心の座標ベクトル．
	ex	トーラスの中心の法線ベクトル．
	rr	トーラスの半径(トーラスの中心から断面の円の中心まで)．
	ra	トーラスの断面の円の半径
	cc	線と塗りつぶしの濃度．

Definition at line 982 of file graph.c.

References circle3d(), WSGraph::gp, local2world(), make_WSGraph(), ON, PI, set_vector(), unit_vector(), WSGraph::xs, WSGraph::ys, and WSGraph::zs.

{
    int  i, nn;
    double  dt, th, xx, yy, zz, sn, cs;
    WSGraph vp;
    vector  ve, vo, vz;

    vp = make_WSGraph(2*(rr+ra)+3, 2*(rr+ra)+3, 2*ra+3);
    if (vp.gp==NULL) return;
    nn = (int)(2*PI*(rr+ra)*2);
    dt = 2.0*PI/nn;

    zz = (vp.zs-1)/2.;
    for (i=0; i<nn; i++) {
        th = dt*i;
        sn = sin(th);
        cs = cos(th);
        xx = (vp.xs-1)/2. + rr*cs;
        yy = (vp.ys-1)/2. - rr*sn;
        vo = set_vector(xx, yy, zz);
        ve = set_vector(sn, cs, 0.0);
        circle3d(vp, vo, ve, ra, cc, ON);
    }
    vz = set_vector((vp.xs-1)/2., (vp.ys-1)/2., (vp.zs-1)/2.);
    ex = unit_vector(ex);

    local2world(gd, vp, ox, vz, ex, NULL, NULL);
    free(vp.gp);
    return;
}

Here is the call graph for this function:

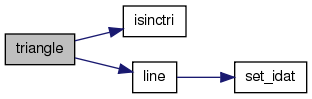
void triangle	(	WSGraph	vp,
		int	x1,
		int	y1,
		int	x2,
		int	y2,
		int	x3,
		int	y3,
		int	cc,
		int	mode
	)

void triangle(WSGraph vp, int x1, int y1, int x2, int y2, int x3, int y3, int cc, int mode)

2Dの三角形の描画．
点(x1,y1),(x2,y2),(x3,y3)の三点を頂点とした三角形を描く．
線の濃度は cc． modeが 1以上なら，三角形の内部を塗りつぶす．

Parameters:

	vp	操作対象となるグラフィックデータ構造体．
	(x1,y1),(x2,y2),(x3,y3)	三角形の頂点の座標．
	cc	線の濃度．
	mode	ON なら三角形の内部の0〜ccをccで塗りつぶす．

使用例

// (100,100),(100,200),(200,100)を頂点とした三角形(直角三角形)を描き，内部を塗りつぶす 
triangle(vp, 100, 100, 100, 200, 200, 100, 1000, ON); 

Definition at line 536 of file graph.c.

References isinctri(), line(), Max, Min, ON, and Px.

{
    line(vp, x1, y1, x2, y2, cc);
    line(vp, x2, y2, x3, y3, cc);
    line(vp, x3, y3, x1, y1, cc);

    if (mode==ON) {
        int i, j, minx, miny, maxx, maxy;
        minx = maxx = x1;
        miny = maxy = y1;
        minx = Min(x2, minx);
        minx = Min(x3, minx);
        miny = Min(y2, miny);
        miny = Min(y3, miny);
        maxx = Max(x2, maxx);
        maxx = Max(x3, maxx);
        maxy = Max(y2, maxy);
        maxy = Max(y3, maxy);
    
        for (j=miny; j<=maxy; j++) {
            for (i=minx; i<=maxx; i++) {
                if (isinctri(x1, y1, x2, y2, x3, y3, i, j)) Px(vp, i, j) = cc;
            }
        }
    }
    return;
}

Here is the call graph for this function:

WSGraph x_reverse_wsg

(

WSGraph

vp

)

WSGraph x_reverse_wsg(WSGraph vp)

グラフィックデータの x軸を反転させる．

Parameters:

vp

操作対象となるグラフィックデータ構造体．

Returns:

反転したグラフィックデータ．

Definition at line 1097 of file graph.c.

References WSGraph::gp, JBXL_GRAPH_MEMORY_ERROR, make_WSGraph(), WSGraph::state, WSGraph::xs, and WSGraph::ys.

{
    int  i, j, cy;
    WSGraph  wp;

    wp = make_WSGraph(vp.xs, vp.ys, 1);
    if (wp.gp==NULL) {
        memset(&wp, 0, sizeof(WSGraph));
        wp.state = JBXL_GRAPH_MEMORY_ERROR;
        return wp;
    }

    for (j=0; j<vp.ys; j++) {
        cy = j*vp.xs;
        for (i=0; i<vp.xs; i++) {
            wp.gp[cy +i] = vp.gp[cy + vp.xs - 1 - i];
        }
    }
    return wp;
}

Here is the call graph for this function:

WSGraph zoom_WSGraph	(	WSGraph	vp,
		int	zm,
		int	mode
	)

WSGraph zoom_WSGraph(WSGraph vp, int zm, int mode)

グラフィックデータ拡大する．

Parameters:

	vp	変換する Word型単純グラフィックデータ．
	zm	倍率．
	mode	モード．1: 線形補間拡大，その他: 単純拡大

Returns:

拡大したグラフィックデータ．

Definition at line 1271 of file graph.c.

References WSGraph::gp, JBXL_GRAPH_IVDARG_ERROR, JBXL_GRAPH_MEMORY_ERROR, make_WSGraph(), WSGraph::state, WSGraph::xs, and WSGraph::ys.

{
    WSGraph  vx;
    int  i, j, k, l, m, n;
    sWord ws, wt;

    memset(&vx, 0, sizeof(WSGraph));
    if (zm<1) {
        vx.state = JBXL_GRAPH_IVDARG_ERROR;
        return vx;
    }

    vx = make_WSGraph(vp.xs*zm, vp.ys*zm, 1);
    if (vx.gp==NULL) {
        memset(&vx, 0, sizeof(WSGraph));
        vx.state = JBXL_GRAPH_MEMORY_ERROR;
        return vx;
    }

    if (mode==1){
        for(j=0; j<vp.ys; j++) {
            for(i=0; i<vp.xs; i++) {
                m = i + j*vp.xs;
                n = (i + j*vx.xs)*zm;
                if(i==vp.xs-1) wt = 0;
                else           wt = (vp.gp[m+1] - vp.gp[m])/zm;
                if(j==vp.ys-1) ws = 0;
                else           ws = (vp.gp[m+vp.xs] - vp.gp[m])/zm;

                for(k=0; k<zm; k++) {
                    for(l=0; l<zm; l++) {
                        vx.gp[n+l+k*vx.xs] = ws*k + wt*l + vp.gp[m];
                    }
                }
            }
        }
    }
    else {
        for(j=0; j<vp.ys; j++) {
            for(i=0; i<vp.xs; i++) {
                m = i + j*vp.xs;
                n = (i + j*vx.xs)*zm;
                for(k=0; k<zm; k++) {
                    for(l=0; l<zm; l++) {
                        vx.gp[n+l+k*vx.xs] = vp.gp[m];
                    }
                }
            }
        }
    }
    return vx;
}

Here is the call graph for this function: